Gráficos Básicos
gráficos de barra
gráficos de linha / interação
gráficos lado a lado
histograma, linhas
Algumas opções para customizar o seu gráfico
Gráficos 3D
11 de outubro de 2024
Aula de Hoje
Gráficos Básicos
Gráficos no R
A função básica para fazer um gráfico no R é o
plot().Os primeiros argumentos serão os pontos a serem plotados.
Em seguida, podemos especificar algumas opções como:
os limites dos eixos com
xlimouylim;usar a escala logarítmica com
log="y";o tipo de linha com
lty, o tipo de símbolo para os pontos compche a cor comcol.
Gráficos no R
Depois de fazer o gráfico básico, podemos adicionar elementos como:
linhas usando o comando
abline();curvas com o comando
lines();pontos com o comando
points();polígonos com o comando
polygon();legenda com o comando
legend().
Gráficos Básicos
- Antes de ver as opções para customizar os gráficos, vamos ver alguns tipos de gráficos com comandos específicos para algumas classes de dados.
Gráficos Básicos
- Vamos usar novamente o banco de dados de ciclones tropicais nos EUA entre 1899-2006.
StormMax = read.table("../datasets/extremedatasince1899.csv", header=T, sep=",")
attach(StormMax)
- Vamos contar o número de ciclones por década:
table( trunc(Yr/10)*10 )[-1]
## ## 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000 ## 183 144 123 204 191 199 179 186 178 191 212
Gráficos de Barra
barplot( table( trunc(Yr/10)*10 )[-1] )
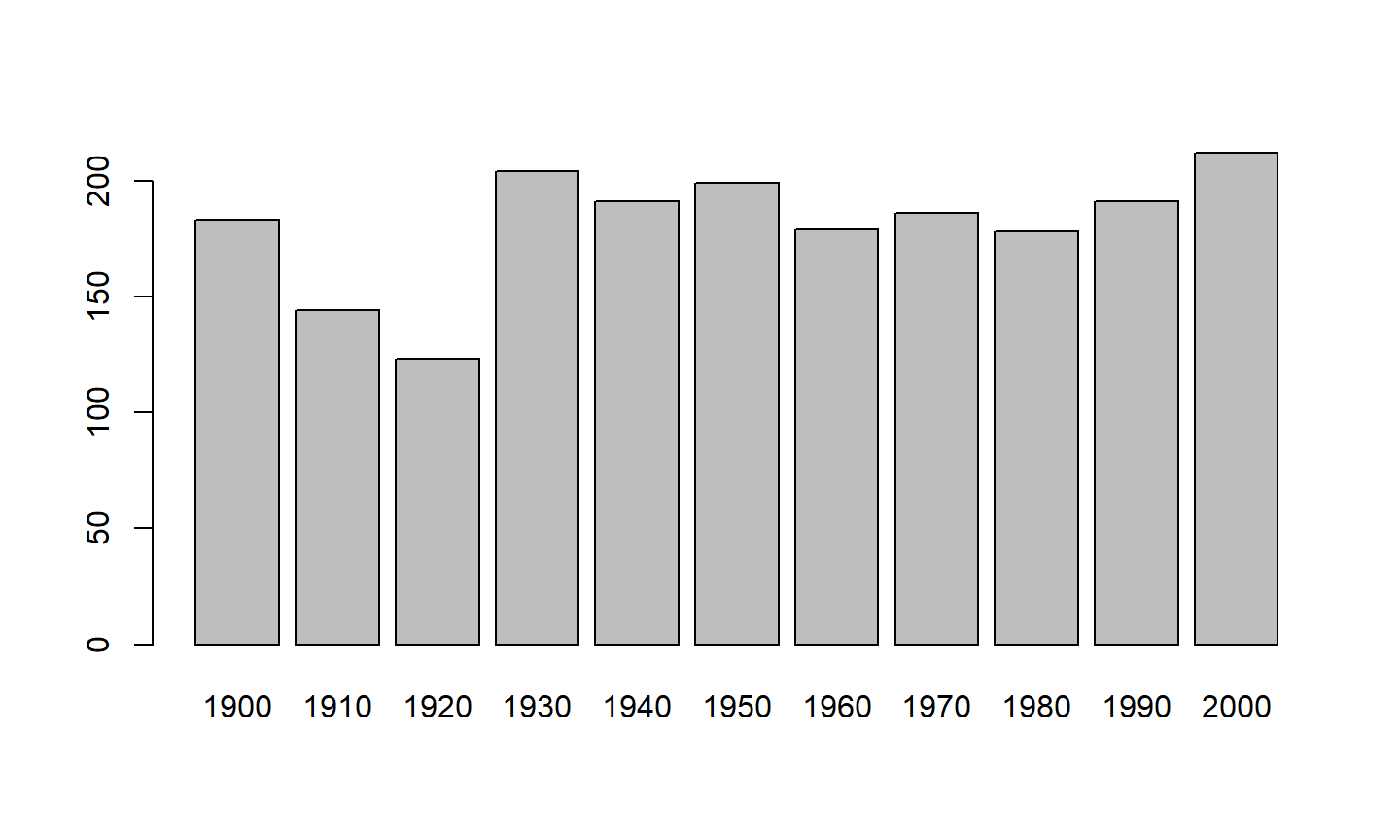
Gráficos de Barra
Exercício
Olhe as opções dos argumentos da função
barplot()no help.Refaça o gráfico anterior alterando:
cor das barras;
título e nome dos eixos;
adicione uma linha com o número médio de ciclones por década.
Gráficos de linhas
decade = trunc(Yr/10)*10 interaction.plot(decade, Region, Wmax, type="b", pch=1:5)
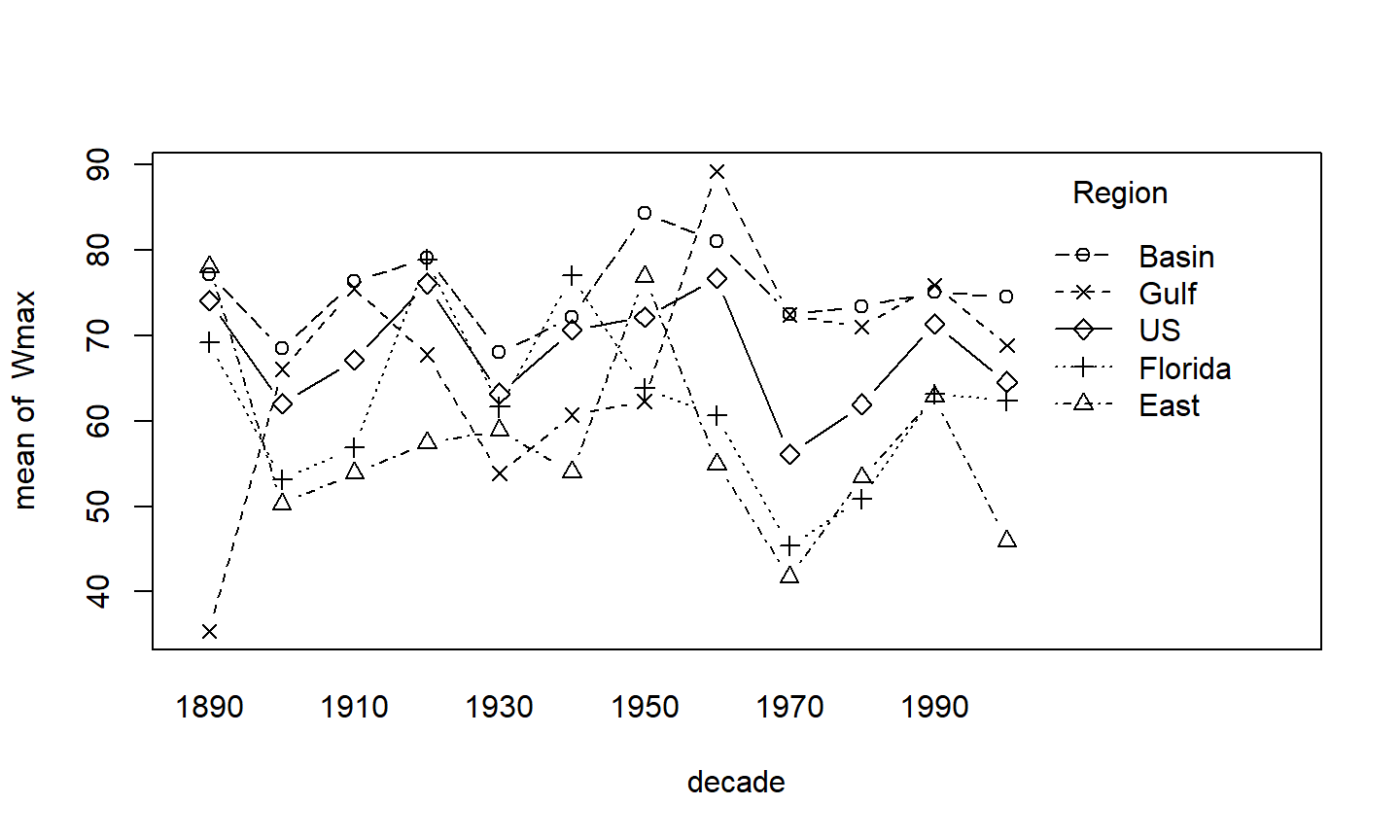
Gráficos de linhas
A função
interaction.plotfaz na verdade, o gráfico de uma estatística descritiva (default é a média) de uma variável resposta (numérica) para as interações de duas variáveis categóricas.O primeiro argumento é
x.factorpara a variável categórica no eixo x;O segundo argumento é
trace.factorcom as categorias para as linhas;O terceiro argumento é
responsecom a variável resposta.
Gráficos de linhas
No gráfico anterior, escolhemos
type="b"para plotar os pontos e linhas entre as observações, e escolhemos os símbolos de 1:5 para os pontos de diferentes categorias.Outros símbolos (de 1 a 20):

Gráficos de linhas
Exercício
Olhe as opções dos argumentos da função
interaction.plot()no help.Refaça o gráfico acima alterando:
símbolos, cor e tipo das linhas;
título e nome dos eixos;
plote a velocidade máxima dos ciclones da década, ao invés da velocidade média.
Gráficos lado a lado
- Histograma e função de distribuição empírica de uma amostra da normal padrão:
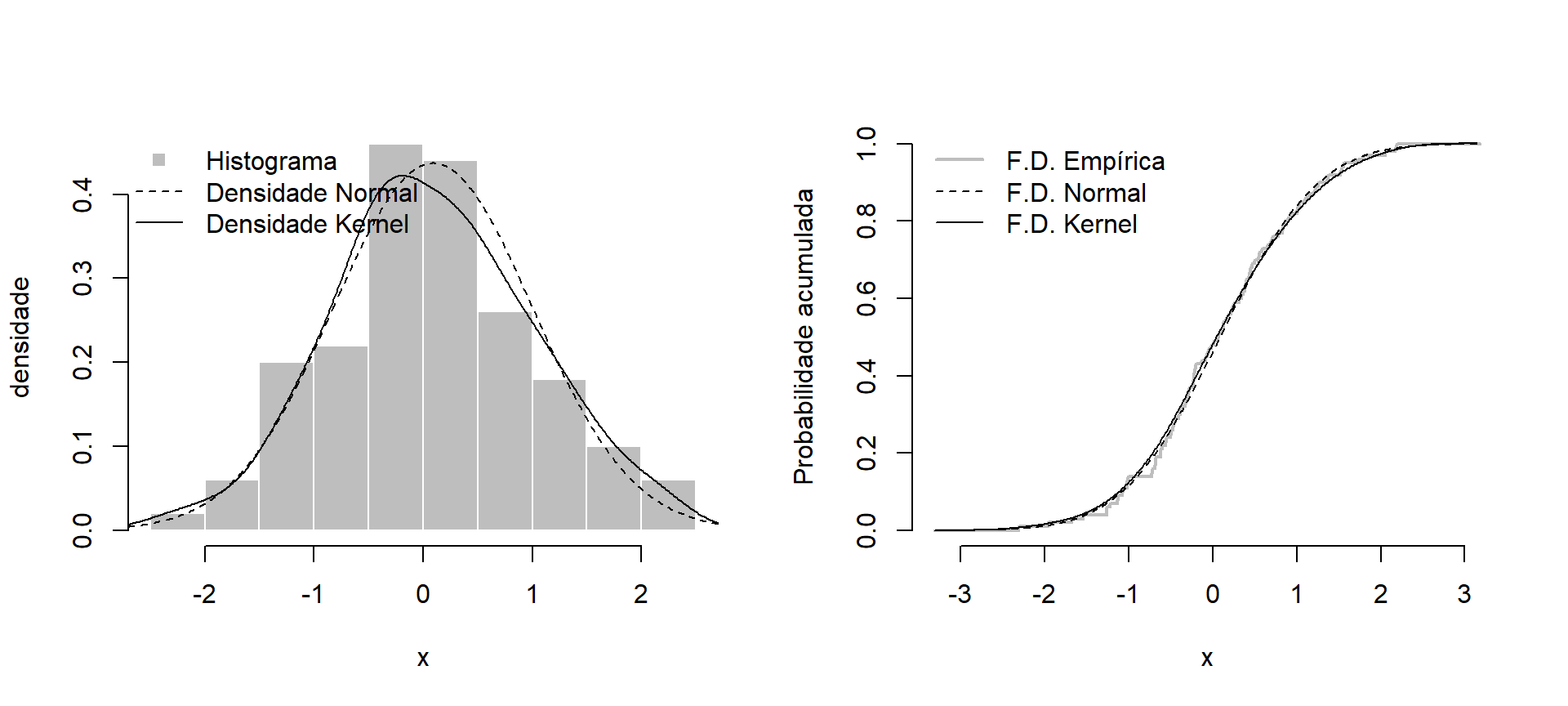
set.seed(123)
x = rnorm(100) # gerando amostra
par(mfrow=c(1,2)) # plotar com 1 linha e 2 colunas
## grafico 1: histograma
hist(x, xlab="x", ylab="densidade", main="", col="grey", border="white", probability=T)
# adicionar linhas da densidade (normal com estimadores de momentos)
u = seq(min(x)-1, max(x)+1, by=.01)
lines(u, dnorm(u,mean(x),sd(x)), lty=2)
# densidade estimada com kernel da normal
d = density(x)
lines(d$x, d$y)
# adicionar legenda
legend("topleft", legend=c("Histograma","Densidade Normal", "Densidade Kernel"),
col=c("grey","black","black"), lwd=c(NA,1,1), lty=c(NA,2,1),
pch=c(15,NA,NA), bty="n")
## grafico 2: função de distribuição empírica
F.empirica = function(y){
mean(x<=y)
}
plot(u, Vectorize(F.empirica)(u), type="s", lwd=2, col="grey",
xlab="x", ylab="Probabilidade acumulada", main="", axes=FALSE)
axis(1); axis(2) # adicionar eixos
lines(d$x, cumsum(d$y)*diff(d$x)[1]) # f.d. kernel
lines(u, pnorm(u,mean(x),sd(x)), lty=2) # f.d. normal
# adicionar legenda
legend("topleft", c("F.D. Empírica", "F.D. Normal", "F.D. Kernel"),
col=c("grey","black","black"), lwd=c(2,1,1), lty=c(1,2,1), bty="n")
Gráficos para classes de objetos
- É possível utilizar as funções básicas de gráficos do R para plotar informações de objetos mais complexos, como a saída de uma regressão:
# selecionando ciclones que ocorreram após 1977 na região 'Basin' StormMax.Basin = subset(StormMax, (Region=="Basin")&(Yr>1977)) attach(StormMax.Basin)
## Os seguintes objetos são mascarados por StormMax: ## ## nao, Region, soi, split, sst, sstmda, sun, Wmax, Yr
Gráficos para classes de objetos
- Boxplot da velocidade de ciclones por ano (para a região “Basin”):
boxplot(Wmax ~ as.factor(Yr), xlab="Ano", ylab="Velocidade (nós)", col="grey")
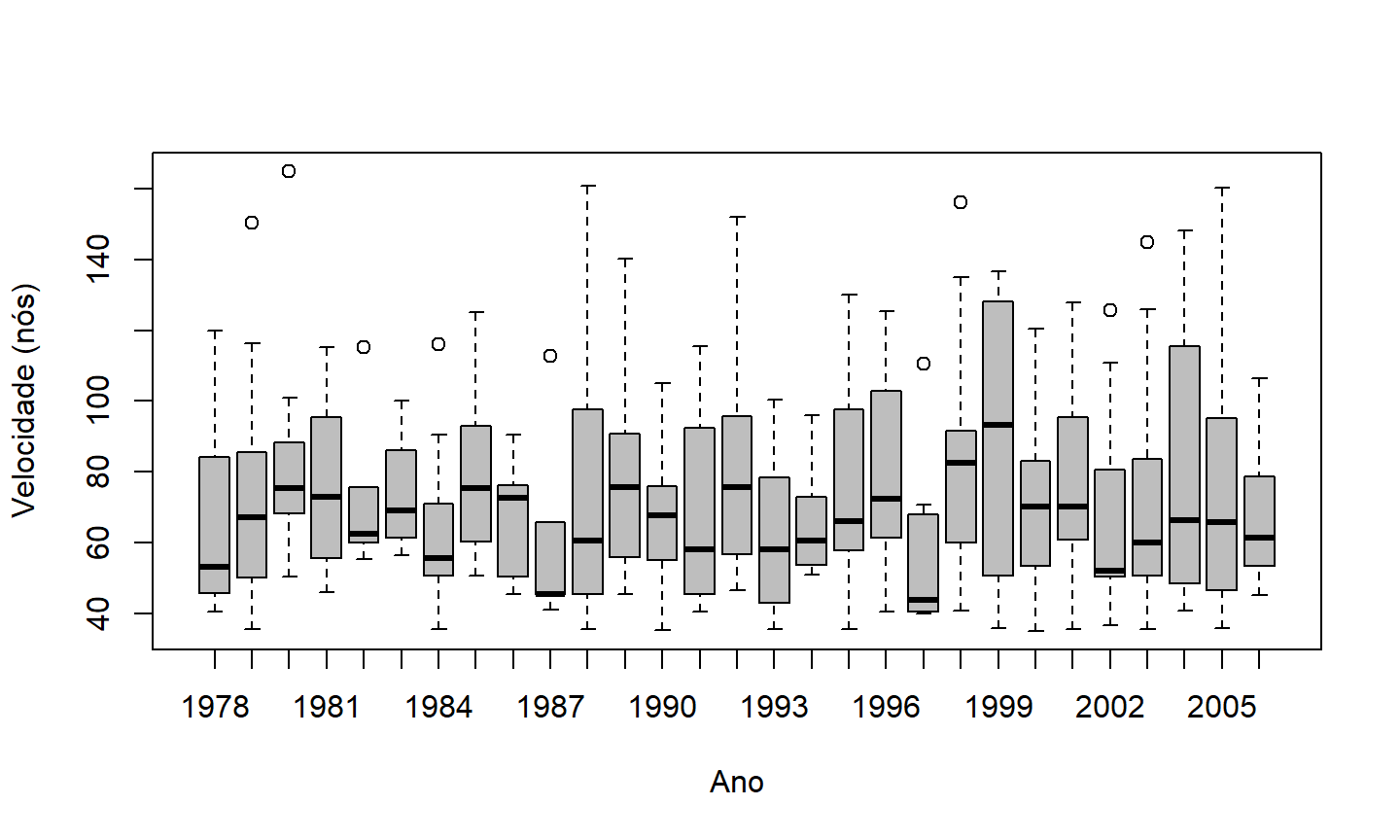
Gráficos para classes de objetos
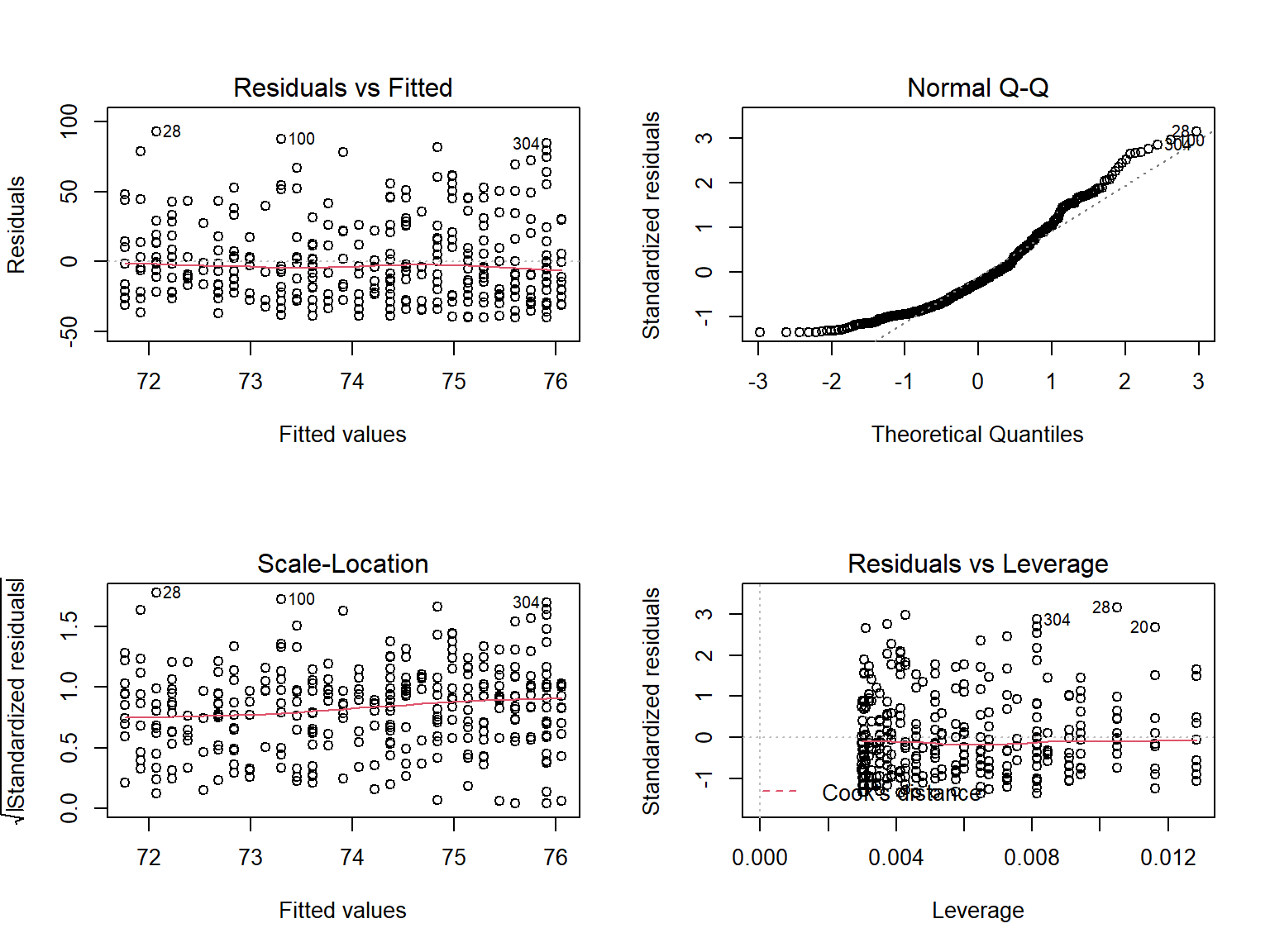
Para objetos do tipo
lm, a funçãoplot()retorna alguns gráficos de diagnóstico do modelo:Para ver o help específico para esse caso, usar
?plot.lm
# regressão linear entre velocidade do vento e ano model = lm(Wmax ~ Yr) par(mfrow=c(2,2)) plot(model)
Gráficos 3D
Gráficos 3D
Para visualizar como fazer gráficos 3D, vamos considerar uma distribuição normal bivariada.
A densidade de uma normal bivariada com médias zero e variâncias um é dada por:
\[f(x,y) = \frac{1}{2\pi\sqrt{1-\rho^2}} \exp\left( -\frac{1}{2(1-\rho^2)}[x^2 + y^2 - 2\rho x y] \right) \qquad \forall x,y \in \mathbb{R}^2 \]
binorm = function(x1,x2,r=0){
exp( -(x1^2 + x2^2 - 2*r*x1*x2)/( 2*(1-r^2) ) )/( 2*pi*sqrt(1-r^2) )
}
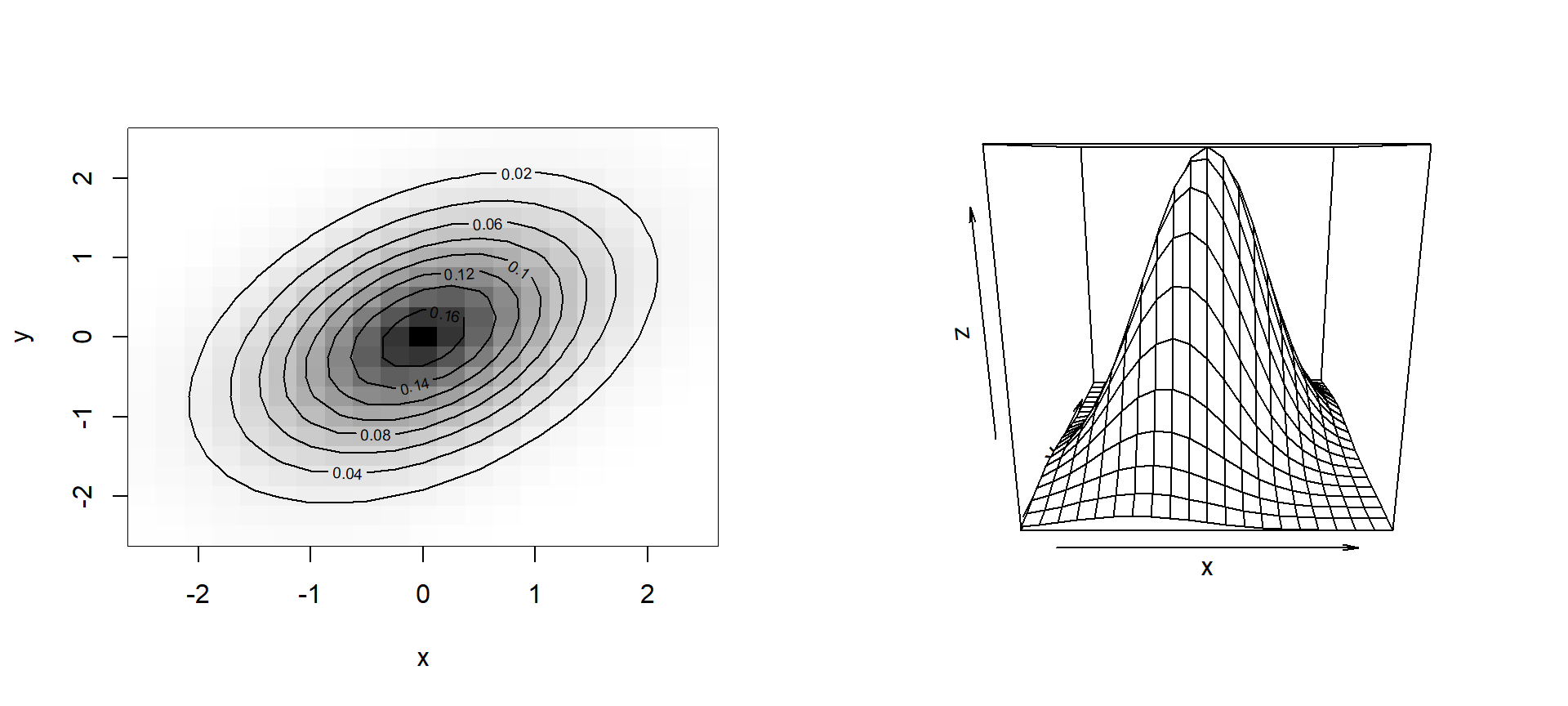
Gráficos 3D
x = y = seq(-2.5, 2.5, by=.25)
z = outer(x, y, function(u,v) binorm(u,v,r=.4))
## para escolher as cores
# install.packages("RColorBrewer")
require(RColorBrewer)
gray.col = gray.colors(n=100, start=0, end=1)
par(mfrow=c(1,2))
# gráfico 1: curva de níveis
image(x, y, z, col=rev(gray.col))
contour(x, y, z, add=TRUE)
# grafico 2: superfície 3D
persp(x, y, z)
Gráficos 3D
Gráficos 3D
- Alterando algumas opções no gráfico da superfície 3D:
persp(x, y, z, theta=210, col=gray.col[45], shade=TRUE)

Gráficos 3D
Exercício
Veja as documentações para as funções utilizadas nos gráficos anteriores.
Refaça os gráficos alterando:
parâmetro de correlação da normal;
quantidade de pontos para criar os vetores
xey;escala de cores (use o comando
display.brewer.all()ou entre no site http://www.colorbrewer.org para ver mais cores).