• Matemática Financeira

  • taxa de juros e taxa de desconto

  • taxa efetiva e nominal

  • fluxo de pagamentos e anuidade certas

• A Matemática Financeira lida com o valor do dinheiro no tempo.

• Vamos ver uma revisão de algumas quantidades e conceitos básicos que precisaremos para avaliar pagamentos futuros.

• Muitas dessas funções estão implementadas no R no pacote lifecontingencies.

• Um capital \(X\) irá valer \(A(t) = X \cdot (1+i)^t\) depois de \(t\) anos, se seguir a lei de juros compostos.

• \(i\) é a taxa de juros efetiva anual, isto é, a quantidade que um investimento irá render após um ano, com juros pagos no final do ano.

• \((1+i)^n\) é chamado de fator de acumulação.

• E se o pagamento dos juros fosse feito antecipadamente (no começo do período)? Os juros recebidos seriam reinvestidos, gerando mais juros, que também seriam investidos… e assim sucessivamente.

• Vamos chamar de taxa de juros antecipados ou taxa de desconto \(d\).

• No final do período, o montante seria \(X + d. X + d^2.X + ... = X \left(\frac{1}{1-d}\right)\) (progressão geométrica).

• A taxa de desconto que leva ao mesmo capital obtido com uma taxa de juros \(i\) é dada por:

\[ X \cdot (1+i) = X \cdot \left( \frac{1}{1-d} \right) \qquad\Rightarrow \qquad d = \frac{i}{1+i} \]

• Por exemplo, qual deve ser a taxa de juros antecipada (ou taxa de desconto) que leva ao mesmo fator de acumulação de uma taxa de juros de 5%?

No R:

0.05/(1+0.05)

## [1] 0.04761905

interest2Discount(i=0.05)

## [1] 0.04761905

• Também podemos ver a taxa de desconto como o valor descontado dos juros \(i\) a serem pagos no final do ano.

\[ d = \frac{i}{1+i} = i \, . \frac{1}{1+i} = i\,.(1-d)\]

Considere um capital investido de 1 unidade. O valor do juros antecipado \(d\) a ser pago é igual ao que renderia de juros postecipado \(i\) aplicado ao capital de \(1-d\).

Equivalentemente, o valor do juros postecipado \(i\) é igual ao que receberia de juros antecipado \(d\) aplicado ao capital de \(1+i\).

\[ i = \frac{d}{1-d} = d \, .(1+i) \qquad \Rightarrow \qquad (1-d) = \frac{1}{1+i} \]

• Juros pode ser pago em frequências maiores do que uma vez por período de tempo.

• Essas frações do período em que os juros são pagos são chamadas de período de conversão.

• Quando o período de conversão é igual à unidade de tempo básica, a taxa de juros (e a de desconto) recebe o nome de taxa efetiva.

• Quando o período de conversão é diferente da unidade de tempo básica, a taxa de juros (e a de desconto) é chamada de taxa nominal.

• Seja \(i\) a taxa de juros efetiva anual.

• Seja \(i^{(m)}\) a taxa de juros nominal anual, convertida em \(m\) vezes por ano.

Logo,

\[ \left( 1 + \frac{i^{(m)}}{m}\right)^m = (1+i) \]

\[ i^{(m)} = m . \left[ (1+i)^{1/m} - 1\right] \]

## Taxa Nominal e Efetiva
nominal2Real(i=0.06, k=12)

## [1] 0.06167781

real2Nominal(i=0.06, k=12)

## [1] 0.05841061

# converter taxa de desconto efetiva para nominal
real2Nominal(i=0.04, k=12, type="discount") 

## [1] 0.04075264

• Valor do montante de 1 unidade acumulado pelo tempo \(t\):

\[A(t) = (1+i)^t = \left( 1 + \frac{i^{(m)}}{m} \right)^{t.m} = \left(1 - \frac{d^{(m)}}{m} \right)^{-t.m} = (1-d)^{-t} = v^{-t} \]

onde \(i\) e \(d\) são as taxas de juros e desconto efetivas, e \(i^{(m)})\) e \(d^{(m)}\) são as taxas nominais.

• Muitas vezes precisamos considerar mais de um pagamento ou pagamentos que são feitos periodicamente.

• Valor Presente: capital em valor atual correspondente a uma série de pagamentos feitos em diferentes tempos.

• Permite comparar em uma mesma base diferentes fluxos de pagamentos. Isso é, podemos avaliar o retorno de diferentes investimentos.

\[VP = \sum_{j=1}^K P_j \,(1+i_j)^{-t_j} \]

onde \(P_j\) é o valor do pagamento e \(i_j\) é a taxa de juros correspondentes ao tempo \(t_j\).

• O pacote lifecontingencies também tem funções para calcular Valor Presente de fluxos de pagamentos determinísticos.

Usando a função presentValue, verifique qual investimento é melhor (com \(i=5\%\)):

1. Pagar $500 agora e receber $100, $200, $300, $250 no final dos próximos quatro anos;

2. Pagar $700 agora e receber $1000 no final do segundo ano.

pg1 = c(-500,100,200,300,250)
t1 = 0:4
(VP1 = presentValue(cashFlows=pg1, t=t1, i=0.05))

## [1] 241.4709

pg2 = c(-700,1000)
t2 = c(0,2)
(VP2 = presentValue(cashFlows=pg2, t=t2, i=0.05))

## [1] 207.0295

Anuidades são fluxos de pagamentos feitos em intervalos regulares de tempo.

• Se os pagamentos são feitos garantidamente durante um tempo, chamamos de anuidades certas.

• Se os pagamentos são feitos no final de cada período, chamamos de anuidades postecipadas (“annuity-immediate”).

• Se os pagamentos são feitos no começo de cada período, chamamos de anuidades antecipadas (“annuity-due”).

• Anuidades também podem ser pagas em pagamentos fracionários dentro de cada período, ou indefinidamente (Bowers et al., 1997; Dickson et al., 2009).

• Anuidade certa postecipada por \(n\) anos:

• Anuidade certa antecipada por \(n\) anos:

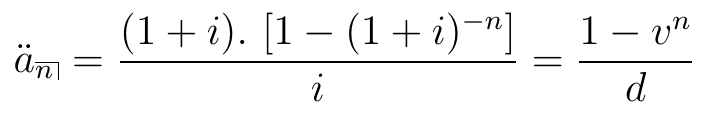
• Perpetuidades (anuidade infinita) antecipada e postecipada:

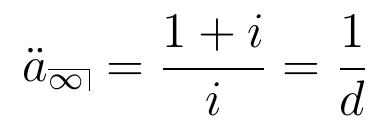
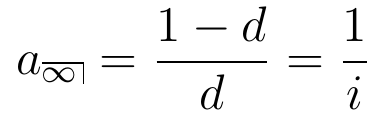
Podemos calcular com a função annuity.

1. Encontre o valor presente de uma anuidade postecipada de $100 paga anualmente por 5 anos, com juros de 9%.
   
   

2. Suponha que uma empresa emita um contrato de dividendo de ações que paga $10 no final do ano indefinidamente, com juros de 6%. Qual o valor presente deste contrato?
   
   

3. Qual o valor que você deve investir hoje, com juros compostos anuais de 6%, para sacar $5000 no começo de cada ano nos próximos 5 anos?

i = 0.09
n = 5
100*(1-(1+i)^(-n))/i

## [1] 388.9651

100*annuity(i=0.09, n=5, type="immediate")

## [1] 388.9651

i = 0.06
10*1/i

## [1] 166.6667

10*annuity(i=0.06, n=Inf)

## [1] 166.6667

i = 0.06
n = 5
5000*(1+i)*(1-(1+i)^(-n))/i

## [1] 22325.53

5000*annuity(i=0.06, n=5, type="due")

## [1] 22325.53

• Também podemos definir o valor acumulado ou valor futuro de uma série de pagamentos.

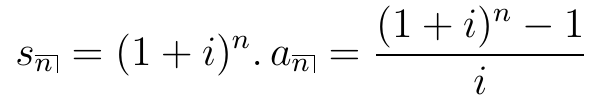
Podemos calcular com a função accumulatedValue.

• Também podemos querer encontrar o valor presente ou valor acumulado de uma série de pagamentos não constantes.

• Todos os casos podem ser avaliados com a fórmula do VP que vimos no começo da aula.

• Mas vamos encontrar expressões para alguns casos específicos, como anuidades aritmeticamente crescentes \((I\ddot{a})_n\) e anuidades aritmeticamente decrescentes \((D\ddot{a})_n\).

• No R: increasingAnnuity e decreasingAnnuity.

• Os seguintes pagamentos serão recebidos:

  • $500 no final do primeiro ano, $520 no final do segundo ano, $540 no final do terceiro ano, e assim por diante, até o pagamento final de $800.

• Considerando uma taxa de juros anual de 2%, encontre o valor presente desses pagamentos no \(t=0\).

• Encontre o valor acumulado desses pagamentos no momento do último pagamento.

Podemos considerar uma anuidade fixa de $480 mais uma anuidade crescente de $20:

480*annuity(i=0.02,n=16)+ 20*increasingAnnuity(i=0.02,n=16)

## [1] 8711.431

Valor acumulado:

(480*annuity(i=0.02,n=16)+ 20*increasingAnnuity(i=0.02,n=16))*1.02^16

## [1] 11958.93

• Dizemos que uma anuidade certa é diferida se o momento de início dos pagamentos é diferente do momento em que estamos avaliando o fluxo de pagamentos.

• Isto é, a sequência de pagamentos só começará daqui a um determinado tempo (chamado de período de diferimento).

• Encontre o valor presente de uma anuidade antecipada que paga $1200 anualmente por 12 anos, com o primeiro pagamento daqui a dois anos. Considere i=6%.

1200*annuity(i=0.06,n=12,m=1,type="immediate")

## [1] 9491.144

1200*annuity(i=0.06,n=12,m=2,type="due")

## [1] 9491.144