Fluxos de pagamentos probabilísticos
Tabela de Vida
criando e manipulando tabelas de vida no R
avaliando probabilidades, esperanças de vida
Suposições para idades fracionárias
Múltiplas Vidas
05 de maio de 2023
Aula de Hoje
Fluxos de pagamentos
Na aula passada, consideramos fluxos de pagamentos determinísticos, isto é, os pagamentos periódicos são feitos com probabilidade 1.
No entanto, nas Ciências Atuariais, muitas vezes teremos que avaliar fluxos de pagamentos probabilísticos.
Pagamentos podem depender da sobrevivência ou morte de um indivíduo (ou grupo de indivíduos).
Fluxos de pagamentos
Para comparar pagamentos ou fluxos de pagamentos em tempos diferentes \(\Rightarrow\) valor presente.
Para comparar pagamentos ou fluxos de pagamentos probabilísticos \(\Rightarrow\) esperança.
Vamos denominar o valor presente desses fluxos de pagamentos como VPA - Valor Presente Atuarial.
Fluxos de pagamentos
O Valor Presente do fluxo de pagamentos probabilístico será uma variável aleatória, vai depender de quando os pagamentos são feitos.
Se os pagamentos dependem da sobrevivência ou morte de um indivíduo, vamos precisar determinar a variável aleatória \(T(x)\): tempo de vida futura de um indivíduo de idade \(x\).
O Valor Presente será uma função de \(T(x)\).
Assim, precisamos encontrar a distribuição de probabilidade de \(T(x)\).
Tabela de Vida
Tabela de Vida
Uma tabela de vida é uma sequência não-crescente de \(l_x\), para as idades \(x=0,1,\dots,\omega\) com a idade terminal \(\omega\).
Cada quantia \(l_x\) representa o número de indivíduos vivos à idade \(x\).
O número \(l_0\) de indivíduos vivos no tempo 0 é a raiz da tabela.
Como a tabela contém o número de sobreviventes, podemos usar os valores de \(l_x\) para calcular as probabilidades de sobrevivência.
Tabela de Vida
- Probabilidade de \((x)\) sobreviver à idade \(x+t\):
\[{}_{t}p_x = P(T(x)>t) = \frac{l_{x+t}}{l_x} \]
- Probabilidade de \((x)\) não atingir a idade \(x+t\):
\[{}_{t}q_x = 1 - {}_{t}p_x = P(T(x) \leq t) = \frac{l_x - l_{x+t}}{l_x} \]
- Notação: a probabilidade \({}_{1}p_x\) será denotada por \(p_x\).
Tabela de Vida
- Podemos criar uma tabela de vida no R usando o pacote
lifecontingenciesde algumas maneiras diferentes:
- imputar diretamente \(x\) e \(l_x\):
tab1 = new("lifetable", x=seq(0,10,1),
lx=seq(from=1000,to=0,by=-100),name="Sample life table 1")
Exercício 1
Verifique o que é o objeto
tab1? Quais quantidades foram passadas (input) e quais foram criadas (output)?Qual a classe desse objeto? Verifique o help da classe para ver os detalhes sobre esse tipo de objeto.
O que a função
summary(tab1)faz? E a funçãoplot(tab1)? Veja quais outros métodos estão implementados para essa classe.
Tabela de Vida
- Podemos criar uma tabela de vida no R usando o pacote
lifecontingenciesde algumas maneiras diferentes:
2 . a partir das probabilidades \(p_x\) ou \(q_x\):
tab2 = probs2lifetable(probs=seq(from=0.1,to=1,by=0.1),
radix=100000,type="qx",name="Sample life table 2")
Exercício 2
O que a função
head(tab2)faz? E a funçãotail(tab2)?Verifique o que é o objeto
tab2? Quais quantidades foram passadas (input) e quais foram criadas (output)?
Obs: Podemos exportar um objeto lifetable para um objeto data.frame usando o comando:
## exportando para data.frame tab2.df = as(tab2, "data.frame") class(tab2.df)
## [1] "data.frame"
Tabela de Vida
Podemos fazer várias análises demográficas usando as funções do pacote.
As principais probabilidades que vamos avaliar são:
- a probabilidade de um indivíduo de idade \(x\) sobreviva à idade \(x+t\):
\[{}_{t}p_x\]
- a probabilidade de um indivíduo de idade \(x\) morrer em \(t\) anos:
\[{}_{t}q_x = 1 - {}_{t}p_x\]
Exercício 3
Usando a Tabela Ilustrativa do SOA (Society of Actuaries) usada no Bowers, calcule:
a probabilidade de um indivíduo de idade 65 morrer antes de completar 85 anos;
a probabilidade de um indivíduo de idade 25 sobreviver até os 65 anos.
## carregando a tabela de vida ilustrativa do SOA
data("soa08")
Exercício 3
Obs: Os objetos da classe lifetable são do tipo S4, um tipo de objeto mais recente do R para organizar várias informações. Note que a tabela soa08 contém alguns “slots”. Você pode acessar os slots com os comandos:
slotNames(soa08)
## [1] "x" "lx" "name"
head(soa08@lx)
## [1] 100000.00 97957.83 97826.26 97706.55 97596.74 97495.03
Exercício 3
Vamos calcular:
- a probabilidade de um indivíduo de idade 65 morrer antes de completar 85 anos;
## prob de (65) morrer em 20 anos (soa08@lx[soa08@x==65]-soa08@lx[soa08@x==85])/soa08@lx[soa08@x==65]
## [1] 0.6869847
qxt(soa08, 65,20)
## [1] 0.6869847
Exercício 3
Vamos calcular:
- a probabilidade de um indivíduo de idade 25 sobreviver até os 65 anos.
## prob de (25) sobreviver 65 anos ##
## [1] 0.7876582
Esperança de vida
- Esperança de vida em anos completos:
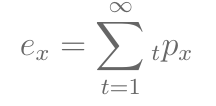
- Esperança de vida em anos completos entre as idades \(x\) e \(x+n\):
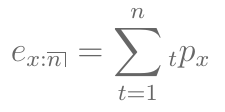
Exercício 4
Usando a Tabela Ilustrativa do SOA, calcule:
a esperança de vida em anos completos ao nascer;
a esperança de vida em anos completos entre as idades 50 e 60.
Exercício 4
- Para a esperança de vida em anos completos ao nascer, só precisamos somar todos os \({}_{t}p_0\)’s. Isso é equivalente a somar todos os valores de \(l_x\), exceto o primeiro, e dividir por \(l_0\).
sum(soa08@lx[soa08@x%in%(1:110)]/soa08@lx[soa08@x==0])
## [1] 71.30788
sum(soa08@lx/soa08@lx[soa08@x==0])-1
## [1] 71.30789
exn(object=soa08)
## [1] 71.30789
Exercício 4
- Para a esperança de vida em anos completos entre as idades 50 e 60, também podemos somar os valores de \(l_x\):
sum(soa08@lx[soa08@x%in%(51:60)]/soa08@lx[soa08@x==50])
## [1] 9.583979
exn(object=soa08, x=50, n=10, type="curtate")
## [1] 9.583979
Esperança de vida
- Esperança de vida completa:
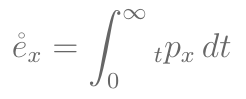
- Esperança de vida completa entre as idades \(x\) e \(x+n\):
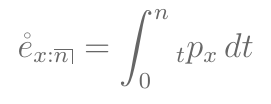
Exercício 5
- Calcule a esperança completa de vida entre as idades 80 e 90.
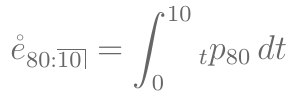
Como vamos calcular essa esperança? Só temos \({}_{t}p_x\) para idades inteiras!
Precisamos assumir que as mortes ocorrem no meio do ano.
Exercício 5
\[\frac 1 2 \cdot \left( \frac{l_{81}+l_{82}+\dots+l_{90}}{l_{80}} + \frac{l_{80}+l_{81}+\dots+l_{89}}{l_{80}} \right)\]
(sum(soa08@lx[soa08@x%in%(81:90)]/soa08@lx[soa08@x==80])+ sum(soa08@lx[soa08@x%in%(80:89)]/soa08@lx[soa08@x==80]))/2
## [1] 6.136299
exn(soa08,80,10,"complete")
## [1] 6.136299
Suposições para idades fracionárias
Suposições para idades fracionárias
Vamos relembrar as suposições sobre a mortalidade em idades fracionárias:
- Distribuição uniforme ou interpolação linear:
Seja \(h \geq 0\) o tempo fracionário, e \(\lfloor h \rfloor\) sua a parte inteira. A interpolação linear entre \({}_{\lfloor h \rfloor}p_x\) e \({}_{\lfloor h \rfloor +1}p_x\) é dada por:
\[{}_{h}\tilde{p}_x = \left( 1 - h + \lfloor h \rfloor \right).\,{}_{\lfloor h \rfloor}p_x + \left( h - \lfloor h \rfloor \right).\,{}_{\lfloor h \rfloor +1}p_x \]
Suposições para idades fracionárias
Força de mortalidade constante:
Sabemos que \({}_{h}p_x = \exp\left( - \int_0^h \mu_{x+s} \,ds\right)\), onde \(\mu_x\) é a força de mortalidade. Assuma que \(h \in [0,1)\) e que \(\mu_{x+s}\) é constante em \([0,1)\). Então\[{}_{h}\tilde{p}_x = \exp\left( - \int_0^h \mu_{x+s} \,ds\right) = \exp(-\mu_x \cdot h) = (p_x)^h \]
Exercício 6
Avalie a probabilidade de uma vida de idade 80 1/4 morrer no próximo semestre, assumindo:
interpolação linear da mortalidade;
força de mortalidade constante.
qxt(object=soa08, x=80.25, t=0.5, fractional="linear")
## [1] 0.04097297
qxt(object=soa08, x=80.25, t=0.5, fractional="constant force")
## [1] 0.04099054
Múltiplas Vidas
Múltiplas Vidas
O pacote lifecontingencies também tem funções de múltiplas vidas implementadas.
- Status de vida conjunta: tempo até a primeira morte
\[T_{xy} = \min(T_x, T_y) \] \[{}_{t}p_{xy} = P(T_{xy}>t) = P(T_x > t \,\cap\, T_y > t) \]
- Status do último sobrevivente: tempo até a última morte
\[T_{\overline{xy}} = \max(T_x, T_y) \] \[{}_{t}p_{\overline{xy}} = P(T_{\overline{xy}}>t) = P(T_x > t \,\cup\, T_y > t) \]
Múltiplas Vidas
- Assumindo vidas independentes, temos que:
\[{}_{t}p_{xy} = {}_{t}p_x \,\cdot {}_{t}p_y \]
\[{}_{t}p_{\overline{xy}} = {}_{t}p_x + {}_{t}p_y - {}_{t}p_{xy} \]
Exercício 7
Assuma que a Tabela Ilustrativa do SOA se aplica a duas vidas independentes de idade 65 e 60.
Calcule:
a probabilidade que ambos estarão vivos após 20 anos;
a probabilidade que pelo menos um estará vivo após 20 anos;
a esperança de vida conjunta.
Dica: veja as funções pxt, pxyzt e exyzt.
Exercício 7
## a) prob. ambos vivos em 20 anos pxt(soa08, x=65, t=20)*pxt(soa08, x=60, t=20)
## [1] 0.1496391
pxyzt(list(soa08,soa08), x=c(65,60), t=20, status="joint")
## [1] 0.1496391
Exercício 7
## b) prob. pelo menos um vivo em 20 anos 1 - qxt(soa08, x=65, t=20)*qxt(soa08, x=60, t=20)
## [1] 0.641433
pxyzt(list(soa08,soa08), x=c(65,60), t=20, status="last")
## [1] 0.641433
## c) esperança de vida conjunta exyzt(list(soa08,soa08), x=c(65,60), t=20, status="joint")
## [1] 11.08887