Otimização no R
Otimização linear
Otimização quadrática
Otimização não-linear
Bases de Dados
Retornos e Valor do Portfólio
02 de junho de 2023
Aula de Hoje
Alocação de Portfólios
Markowitz (1952) foi um dos primeiros a ver a alocação de porfólios como um problema de otimização. Desde então, esse tópico tem sido bastante estudado e vários modelos foram propostos.
Alocação de portfólios pode ser visto como um método para maximizar o grau de satisfação do investidor.
Por exemplo, um investidor pode estar procurando um portfólio que minimize o risco representado por um estimador da covariância dos retornos diários de ações, enquanto outro investidor pode querer medir o risco como a redução da riqueza em um determinado tempo.
Alocação de Portfólios
Primeiro, vamos ver como fazer otimização no R, o que permite que o usuário implemente sua própria rotina para outros processos.
Depois, serão apresentados exemplos simples para serem entendidos, mas que podem ser estendidos para modelos mais complexos.
Otimização no R
Otimização no R
Vários algoritmos e pacotes existem para resolver problemas de otimização. Vamos focar em um pacote para cada tipo de problema, mas estejam cientes de que existem outras rotinas para um mesmo tipo de otimização.
As rotinas de otimização não-lineares que já estão na base do R são:
optim()enlminb(), que acomodam apenas restrições simples.Outros pacotes:
Rglpk,quadprog,Rsolnp,DEoptim,robustbase.
Otimização linear
Seja \(\mathbf x \in \mathbb{R}^n\) um vetor de variáveis sujeitas a restrições dadas por equações e inequações lineares.
O problema de otimização linear pode ser escrito como:
\[\mbox{minimize}_{\mathbf{x}} \quad \mathbf c' \mathbf{x} \\[.2cm] \mbox{sujeito a:} \quad \mathbf{A}_{eq} \,\mathbf x = \mathbf a_{eq} \quad\mbox{ e }\\ \qquad \quad \mathbf A \, \mathbf x \geq \mathbf a \] onde \(\mathbf{A}_{eq}\) e \(\mathbf{a}_{eq}\) são a matriz e o vetor de coeficientes da restrição da igualdade, \(\mathbf{A}\) e \(\mathbf{a}\) são os coeficientes da restrição da desigualdade, e \(\mathbf{c}\) é o vetor de coeficientes da função que desejamos maximizar/minimizar.
Otimização linear
- Vários pacotes possuem funções implementadas para otimização linear:
https://cran.r-project.org/web/views/Optimization.html
- Vamos usar o pacote
Rglpkque tem funções para otimização linear e programação inteira mista.
Otimização linear
args(Rglpk_solve_LP)
## function (obj, mat, dir, rhs, bounds = NULL, types = NULL, max = FALSE, ## control = list(), ...) ## NULL
onde obj contém os coeficientes da função que queremos otimizar, mat é a matriz com os coeficientes das restrições, dir descreve as direções e tipos de desiguldades, e rhs é o vetor do lado direito (“right hand side”) das restrições.
- A função
LP_solverque está no código da aula prepara os objetos no formato correto e executa a otimização linear de acordo com a fórmula do slide anterior.
Otimização quadrática
Comparado à otimização linear, os problemas de otimização quadrática contém um termo quadrático (\(\mathbf{x}'\mathbf{Q}\,\mathbf{x}\)) na função que desejamos maximizar/minimizar.
Os demais parâmetros permanecem os mesmos.
\[\mbox{minimize}_{\mathbf{x}} \quad \mathbf c' \mathbf{x} + \mathbf{x}'\mathbf{Q}\,\mathbf{x} \\[.2cm] \mbox{sujeito a:} \quad \mathbf{A}_{eq} \,\mathbf x = \mathbf a_{eq} \quad\mbox{ e } \\ \qquad \quad \mathbf A \, \mathbf x \geq \mathbf a \]
Otimização quadrática
- Vários pacotes possuem funções implementadas para otimização quadrática:
https://cran.r-project.org/web/views/Optimization.html
- Vamos usar o pacote
quadprog.
Otimização quadrática
- A função
solve.QPencontra soluções para problemas da forma \(\min_{\mathbf{x}} \left( -\mathbf{c}'\mathbf{x} + \tfrac{1}{2}\, \mathbf{x}' \mathbf{Q}\,\mathbf{x} \right)\) sujeito a \(\mathbf{A}\,\mathbf{x} \geq \mathbf{a}\)
args(solve.QP)
## function (Dmat, dvec, Amat, bvec, meq = 0, factorized = FALSE) ## NULL
onde Dmat é a matriz \(\mathbf{Q}\) do termo quadrático, dvec é o vetor \(\mathbf{c}\) da parte linear, e Amat e bvec são a matriz \(\mathbf{A}\) e o vetor \(\mathbf{a}\) com os coeficientes das restrições.
- A função
QP_solverque está no código da aula prepara os objetos no formato correto e executa a otimização quadrática de acordo com a fórmula do slide anterior.
Otimização não-linear
- Os problemas de otimização não-linear são caracterizados por uma função não-linear \(f(\mathbf{x})\) que desejamos maximizar/minimizar.
\[\mbox{minimize}_{\mathbf{x}} \quad f(\mathbf{x}) \\[.2cm] \mbox{sujeito a:} \quad\,\, \mathbf{A}_{eq} \,\mathbf x = \mathbf a_{eq}, \\ \qquad \qquad \quad \mathbf A \, \mathbf x \geq \mathbf a, \\ \qquad \qquad\, h_i^{eq}(\mathbf{x}) = \,0, \\ \qquad \qquad \,\,\, h_i(\mathbf{x}) \geq \,0. \]
onde \((\mathbf{A}_{eq}, \mathbf{a}_{eq})\) e \((\mathbf{A},\mathbf{a})\) são os coeficientes das restrições lineares, e \(h_i^{eq}\) e \(h_i\) são as restrições não-lineares.
- A função
NLP_solverque está no código da aula prepara os objetos e executa a otimização não-linear usando o pacoteRsolnp.
Base de dados
Base de dados
Algumas bases de dados que vamos usar nos exemplos de otimização:
- Índices de ações européias: base
EuStockMarketsque já vem na configuração base do R. Consiste em índices de ações européias entre 1991 e 1998, incluindo DAX alemão, SMI suíço, CAC francês e FTSE britânico.
- Índices de ações européias: base
data("EuStockMarkets")
head(EuStockMarkets)
## DAX SMI CAC FTSE ## [1,] 1628.75 1678.1 1772.8 2443.6 ## [2,] 1613.63 1688.5 1750.5 2460.2 ## [3,] 1606.51 1678.6 1718.0 2448.2 ## [4,] 1621.04 1684.1 1708.1 2470.4 ## [5,] 1618.16 1686.6 1723.1 2484.7 ## [6,] 1610.61 1671.6 1714.3 2466.8
Base de dados
- Para ilustrar como obter dados de outras fontes, vamos usar também uma base de índices NASDAQ e do tesouro americano.
Primeiro, vá até https://finance.yahoo.com/ e procure pelo código de algum índice (por exemplo,
IXICque é o índice NASDAQ).Clique em Historical Data.
Se quiser, pode selecionar um período específico (por exemplo, 1 ano), e em seguida clique em Download Data.
Você terá um arquivo .csv salvo na pasta de Downloads com as cotações diárias e outras informações do índice selecionado.
Base de dados
## Indice NASDAQ Bank
file = "../datasets/IXIC.csv"
Nas = read.csv(file, colClasses = c("Date", rep("numeric",6)))
head(Nas)
## Date Open High Low Close Adj.Close Volume ## 1 2022-06-01 12176.89 12237.94 11901.43 11994.46 11994.46 4719900000 ## 2 2022-06-02 11945.57 12320.12 11901.45 12316.90 12316.90 4445840000 ## 3 2022-06-03 12097.12 12167.44 11966.62 12012.73 12012.73 4130040000 ## 4 2022-06-06 12200.33 12245.40 12004.20 12061.37 12061.37 4647010000 ## 5 2022-06-07 11925.81 12194.86 11888.61 12175.23 12175.23 4411240000 ## 6 2022-06-08 12147.28 12235.78 12052.70 12086.27 12086.27 4708980000
Retornos
Retornos
A partir dos dados que baixamos, vamos definir algumas quantidades mais apropriadas para modelar com uma distribuição estatística.
Por exemplo, uma das transformações mais comuns é para obter os retornos:
\[ r_t = \frac{P_t - P_{t-1}}{P_{t-1}} = \frac{P_t}{P_{t-1}} - 1 \] onde \(P_t\) é o preço da ação/índice no tempo \(t\).
Retorno Acumulado
- Baseado nos retornos nos tempos \(t\), podemos obter o retorno acumulado no período \(T\) como:
\[r_T = \frac{P_T}{P_0} - 1 = \frac{P_T}{P_{T-1}}\,.\,\frac{P_{T-1}}{P_{T-2}} \dots \frac{P_1}{P_0} - 1 = \prod_{t=1}^T \frac{P_t}{P_{t-1}} - 1\]
Retorno de portfólio
- Considere um portfólio de investimentos no tempo \(t\). Seu valor é dado por:
\[W_t = \sum_i P_{i,t} \] que corresponde à soma dos valores dos seus componentes.
Retorno de portfólio
- O retorno do portfólio é dado por:
\[R_t = \frac{W_t - W_{t-1}}{W_{t-1}} = \frac{[P_{1,t} - P_{1,t-1}]+\dots+[P_{N,t} - P_{N,t-1}]}{W_{t-1}} \\[.5cm] \,\,\qquad\quad =\frac{r_1.P_{1,t-1} + \dots + r_N.P_{N,t-1}}{W_{t-1}} \]
Retorno de portfólio
- Assim, o retorno do portfólio é a soma dos valores dos seus componentes ponderados por \(w_i=\frac{P_{t-1}}{W_{t-1}}\).
\[R_t = \sum_{i=1}^N \frac{P_{t-1}}{W_{t-1}}.r_i = \sum_{i=1}^N w_i .\, r_i \]
Retorno de portfólio
- Calculando os retornos para os nossos dados:
## Retornos
x <- apply(EuStockMarkets, MAR=2,
function(x) x[-1] / x[-length(x)] - 1)
Valor do portfólio
- Dados os retornos \(r_t\) e os pesos \(w_i\), o valor do portfólio no tempo \(t\) pode ser calculado como:
\[W_t = W_0 \,. \prod_{i=1}^t (1 + \mathbf{r}'_t \mathbf{w}) \] onde \(W_0\) é o valor inicial do portfólio.
Valor do portfólio
## Função para calcular o valor do portfólio
pftPerf <- function(x, w, W0 = 1000) {
W0 * cumprod(c(1, 1 + x %*% w))
}
Valor do portfólio
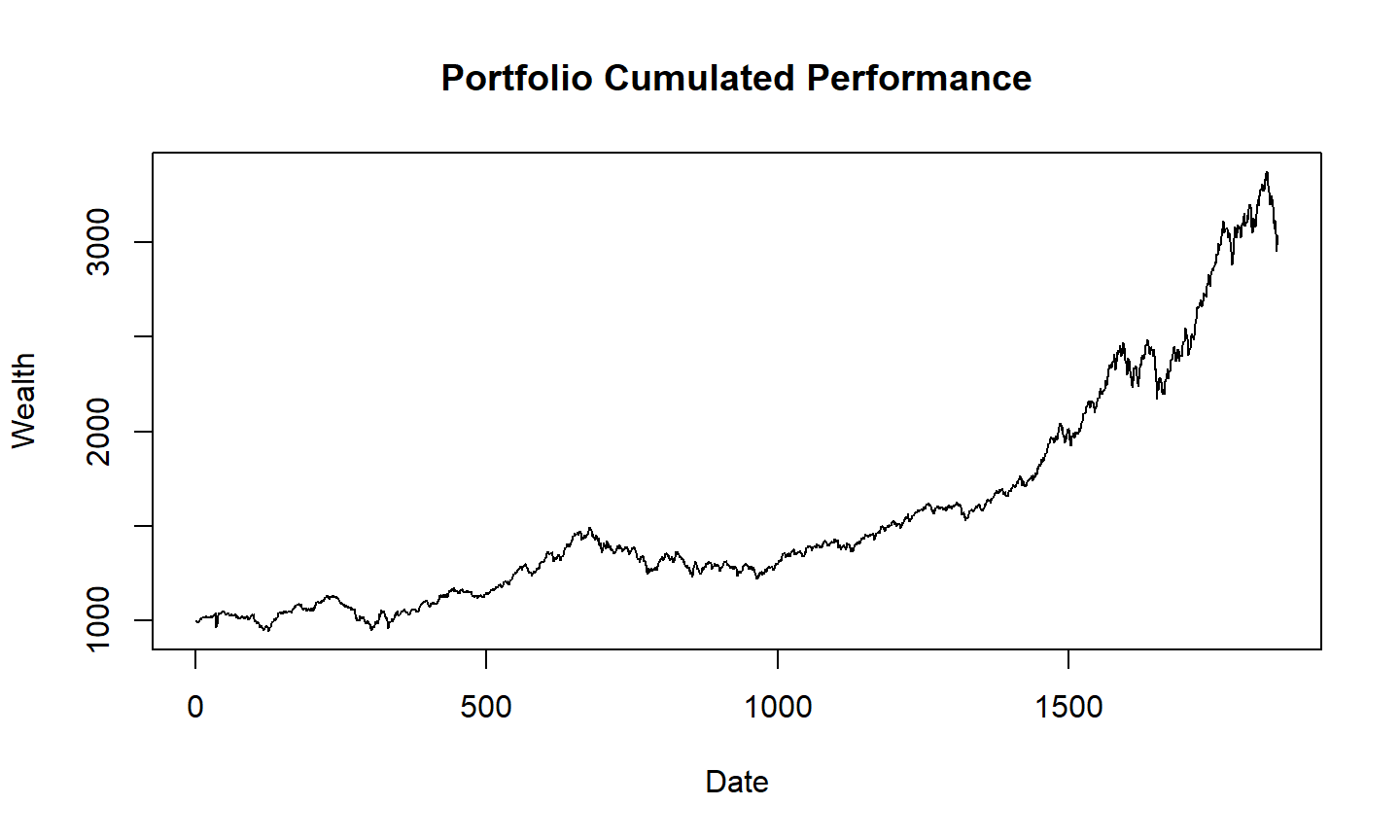
Exercício
Repetir o gráfico usando os dados da NASDAQ.
Nesse caso, assumir um portfólio apenas com este índice (peso de 100%).