• Otimização de portfólios com Restrições

  • Retorno Alvo
  • Investimento Total
  • Posições Long-only
  • Restrições de grupo

• Modelo de Média-Variância

  • Exemplos

• Modelo de Média-Variância Robusto

• Modelo de Mínima Variância

• Otimização de portfólios consiste em minimizar uma medida de risco dado um retorno alvo e restrições operacionais.

• Vamos ver primeiro como implementar alguns tipos comuns de restrições.

• Em seguida, vamos ver o Modelo de Média-Variância, em que a medida de risco é dada pela matriz de covariância do portfólio, e algumas variações deste modelo ilustrados por exemplos.

• Além das medidas de risco, outro ponto importante da otimização de portfólios é a especificação das restrições operacionais ou preferenciais.

• Antes de mostrar os exemplos, vamos ver alguns tipos de restrições que são comuns em alocação de portfólios, e como implementá-las como funções do R.

• Essa restrição vem do objetivo de atingir um retorno alvo com a alocação do portfólio.

• A restrição é dada por:

\[\mu'\mathbf{w} = \bar{r} \]

onde \(\mu\) é o vetor de retornos médios dos componentes do portfólio, \(\mathbf{w}\) são os pesos que desejamos calcular, e \(\bar{r}\) é o retorno alvo.

• Para implementar essa restrição no R, vamos considerar a matriz \(\mathbf{A}_{eq}\) e o vetor \(\mathbf{a}_{eq}\) (da aula passada).

\[ \mathbf{A}_{eq} \,\mathbf{x} = \mathbf{a}_{eq} \]

## Restrição Retorno Alvo
targetReturn <- function(x, target) {
  list(Aeq = rbind(colMeans(x)), aeq = target)
}

• Essa restrição diz que o capital deve estar todo investido no portfólio.

• Corresponde à condição na qual a soma dos pesos \(\mathbf{w}\) deve ser 100%, onde os pesos correspondem à proporção do capital a ser alocado para cada componente.

\[ \mathbf{A}_{eq} \,\mathbf{x} = \mathbf{a}_{eq} \]

## Restrição Investimento Total
fullInvest <- function(x) {
  list(Aeq = matrix(1, nrow = 1, ncol = ncol(x)), aeq = 1)
}

• Essa restrição especifica que o fundo só pode operar com posições compradoras (long = operar “comprado”), isto é, vai receber mais com a valorização dos ativos.

• Isso é diferente de operar “vendido” (short), por exemplo com empréstimo de ações, em que você ganha com a desvalorização dos ativos. Nesse caso, os pesos dos ativos seriam negativos.

• Assim, de acordo com essa restrição, os pesos só podem ser positivos.

\[ \mathbf{A} \,\mathbf{x} \geq \mathbf{a} \]

## Restrição Long Only
longOnly <- function(x) {
  list(A = diag(1, ncol(x)), a = rep(0, ncol(x)))
}

• Essas restrições são derivadas de restrições operacionais que obrigam um investidor a ter uma porcentagem mínima/máximo dos ativos em um determinado grupo de ações.

• Por exemplo:

  • no máximo 10% do portfólio pode estar no setor financeiro ou de bancos;

  • no máximo 30% do portfólio pode estar em um único ativo;

  • no mínimo 10% do portfólio deve estar investido no tesouro nacional.

• Para isso, vamos usar os seguintes índices (Capítulo 13):

• FVX = United States 5-Year Bond Yield;
  
• TYX = United States 30-Year Bond Yield

• Foram extraídos o valor de cada índice entre 01/03/2020 e 01/03/2021 (site: https://www.investing.com)

## Dados NASDAQ
file = "../datasets/nasdaq.csv"
nas = read.csv(file, colClasses = c("Date", rep("numeric",10)))
head(nas)
id = names(nas)[-1]

## calcular retornos
x <- apply(nas[,-1], MAR=2, function(x) x[-1] / x[-length(x)] - 1)
dim(x)

## Restrição de Grupo
GroupBudget <- function() {
  # max 10\% in financial and bank sector
  A1 <- matrix(0, ncol = length(id), nrow = 1)
  colnames(A1) <- id
  A1[1, c("IXBK", "IXF")] <- -1
  a1 <- -0.1
  
  # max 30\% in a single instrument
  A2 <- diag(-1, length(id))
  a2 <- rep(-0.3, length(id))
  
  # at least 10\% in treasury
  A3 <- matrix(0, ncol = length(id), nrow = 1)
  colnames(A3) <- id
  A3[1, c("FVX", "TYX")] <- 1
  a3 <- 0.1
  list(A = rbind(A1, A2, A3), a = c(a1, a2, a3))
}

O Modelo de Média-Variância é um modelo de otimização (Markowitx, 1953) que assume que:

• o portfólio consiste em ativos de risco e ativos sem risco;
• os preços dos ativos são dados e determinados externamente;
• os investidores não influenciam no preço dos ativos;
• os retornos seguem processos estocásticos com distribuições de probabilidade elípticas (parecida com a normal multivariada), o que quer dizer que existe uma matriz de covariância;
• não considera taxas e custos de transações;
• os mercados para todos os ativos são líquidos (é possível convertê-los em dinheiro facilmente);
• os ativos são infinitamente divisíveis;
• e é preciso fazer investimento total.

• A medida de risco proposta por Markowitz é uma matriz de covariância dos ativos ponderada:

\[\mathbf{w}'\, \Sigma \, \mathbf{w} = \sum_i \sum_j w_i \,. w_j \,. \mbox{Cov}(\mathbf{x}_i,\mathbf{x}_j) \] onde \(\Sigma\) é a matriz de covariância e \(\mathbf{w}\) são os pesos do portfólio.

• A otimização é obtida definindo-se um retorno alvo \(\bar{r}\), e as restrições de investimento total e long-only, tal que:

\[\mbox{minimize}_{\mathbf{w}} \qquad \mathbf{w}'\,\Sigma \,\mathbf{w} \qquad \mbox{(risco covariância)} \\[.5cm] \mbox{sujeito a } \qquad \mathbf{w}' \hat{\mu} = \bar{x} \qquad \mbox{(retorno alvo)} \\ \qquad \qquad \qquad \qquad \ \mathbf{w}' \mathbf{1} = 1 \qquad \mbox{(investimento total)} \\ \qquad \qquad \quad \, \mathbf{w} \geq 0 \qquad (long \;only) \]

onde \(\hat{\mu}\) é o vetor dos retornos médios.

• Esse problema não pode ser resolvido analiticamente, por isso precisamos de um algoritmo de otimização.

• O Modelo de Média-Variância é representado por um problema de Otimização Quadrática.

• Vamos usar a função QP_solver definida na última aula.

## Modelo de Média-Variância 
MV_QP <- function(x, target, Sigma = cov(x), ...,
                  cstr = c(fullInvest(x), targetReturn(x, target), longOnly(x), ...),
                  trace = FALSE) {
  
  # quadratic coefficients
  size <- ncol(x)
  c <- rep(0, size)
  Q <- Sigma
  
  # optimization
  sol <- QP_solver(c, Q, cstr, trace)
  
  # extract weights
  weights <- sol$solution
  names(weights) <- colnames(x)
  weights
}

• Na função MV_QP, x são os retornos dos ativos, target é o retorno alvo do portfólio, e Sigma é o estimador clássico de covariância.

• Os demais argumentos são apenas usados para passar as restrições para o problema de otimização.

• Esse modelo pode ser implementado de algumas maneiras diferentes.

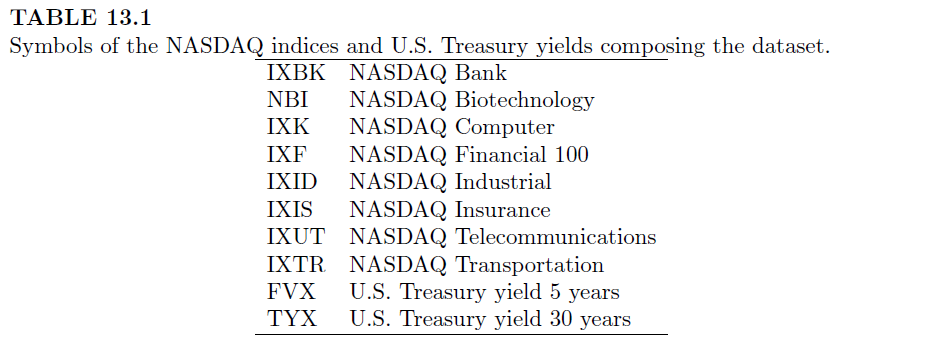
• Vamos testar primeiro o modelo para encontrar os pesos que minimizam a medida de risco usando a média dos retornos de um portfólio uniforme (pesos iguais) como retorno alvo.

## Exemplo - retorno alvo = média dos retornos
w <- MV_QP(x, target=mean(x))
round(w,4) # pesos 'ótimos'

##   IXBK    NBI    IXK    IXF   IXID   IXIS   IXUT   IXTR    FVX    TYX 
## 0.0000 0.2867 0.0000 0.0000 0.0000 0.2509 0.3710 0.0000 0.0914 0.0000

## restrições atendidas?
all.equal( c( t(w)%*%col_means(x) ) , mean(x) )   # retorno alvo
all.equal( sum(w) , 1 )                           # investimento total 
# sum(w) == 1
all(round(w,10) >= 0)                                       # long only

• Pesos que minimizam o risco e atingem o retorno médio:

## modelo de média-variância
t(w)%*%cov(x)%*%w   # covariância
t(w)%*%col_means(x) # retorno

## modelo de pesos uniformes
u = rep(1/10,10)
t(u)%*%cov(x)%*%u   # covariância
t(u)%*%col_means(x) # retorno

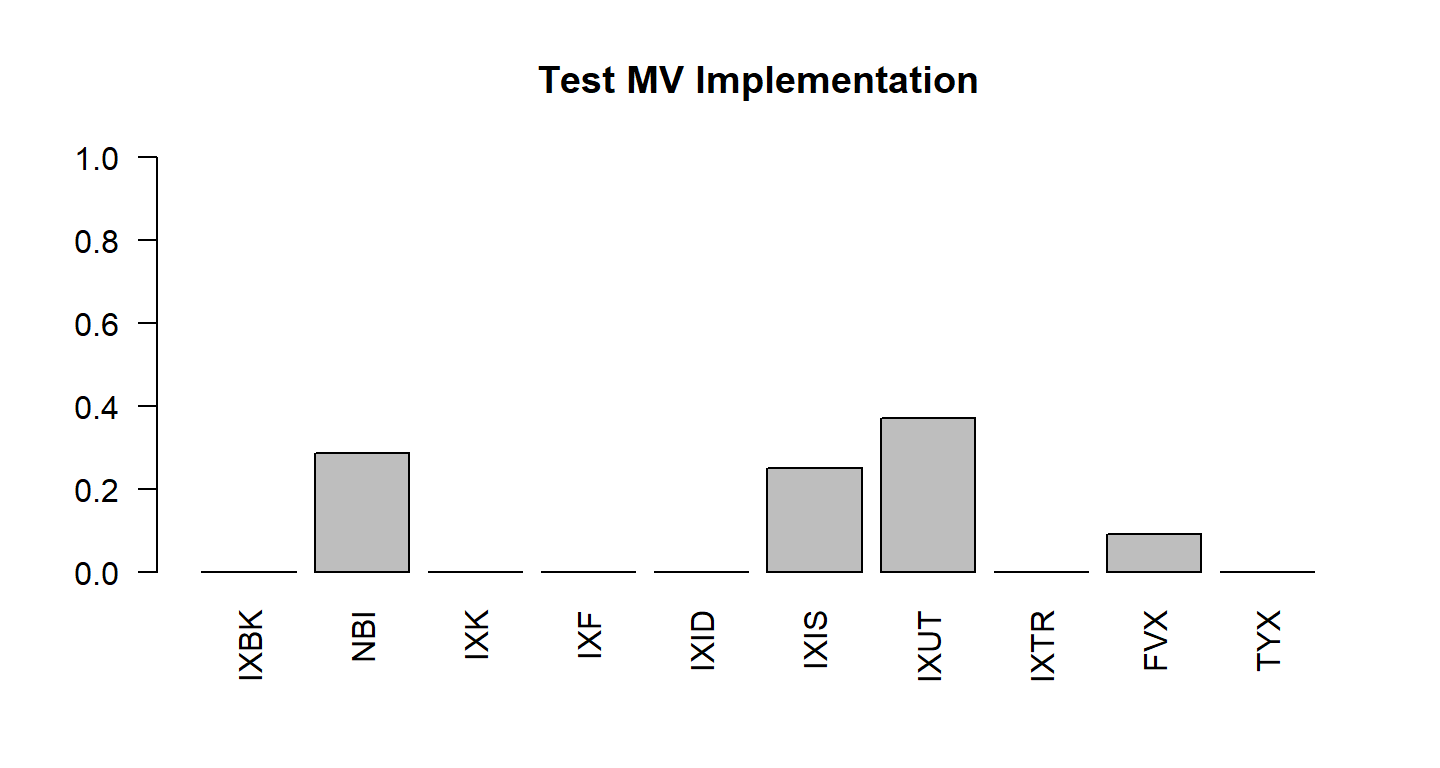
• Vamos fazer outro teste para o nosso modelo.

• Vamos ver o que acontece quando definimos o retorno alvo como o menor retorno médio dentre os ativos.

## Exemplo - retorno alvo = retorno médio mínimo
which(col_means(x)==min(col_means(x)))

## IXID 
##    5

w <- MV_QP(x, target=min(col_means(x)))
round(w, 4)

## restrições atendidas?
all.equal( c(t(w)%*%col_means(x)) , min(col_means(x)) )  # retorno alvo
all.equal(sum(w) , 1)                                    # investimento total 
all(round(w,10) >= 0)                                     # long only
# all(w >= 0)

• Até agora, para rodar a função de otimização de acordo com o Modelo de Média-Variância, só especificamos a matriz de retornos x e o valor do retorno alvo target.

args(MV_QP)

## function (x, target, Sigma = cov(x), ..., cstr = c(fullInvest(x), 
##     targetReturn(x, target), longOnly(x), ...), trace = FALSE) 
## NULL

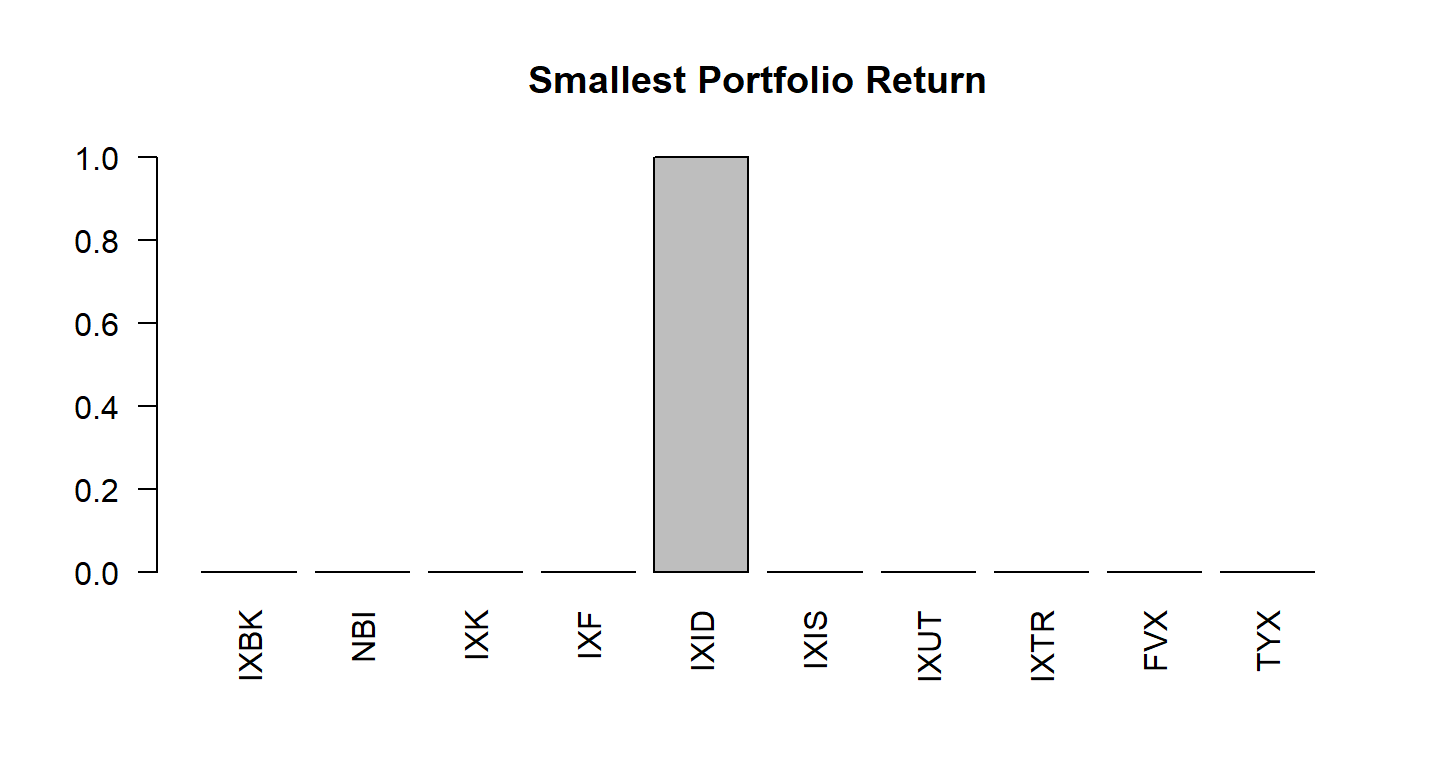
• O argumento cstr passa as restrições default de investimento total, retorno alvo e long-only. Vamos ver agora como especificar mais condições, como as restrições de grupo.

## Exemplo - restrições de grupo
w <- MV_QP(x, mean(x), Sigma = covMcd(x)$cov, GroupBudget())

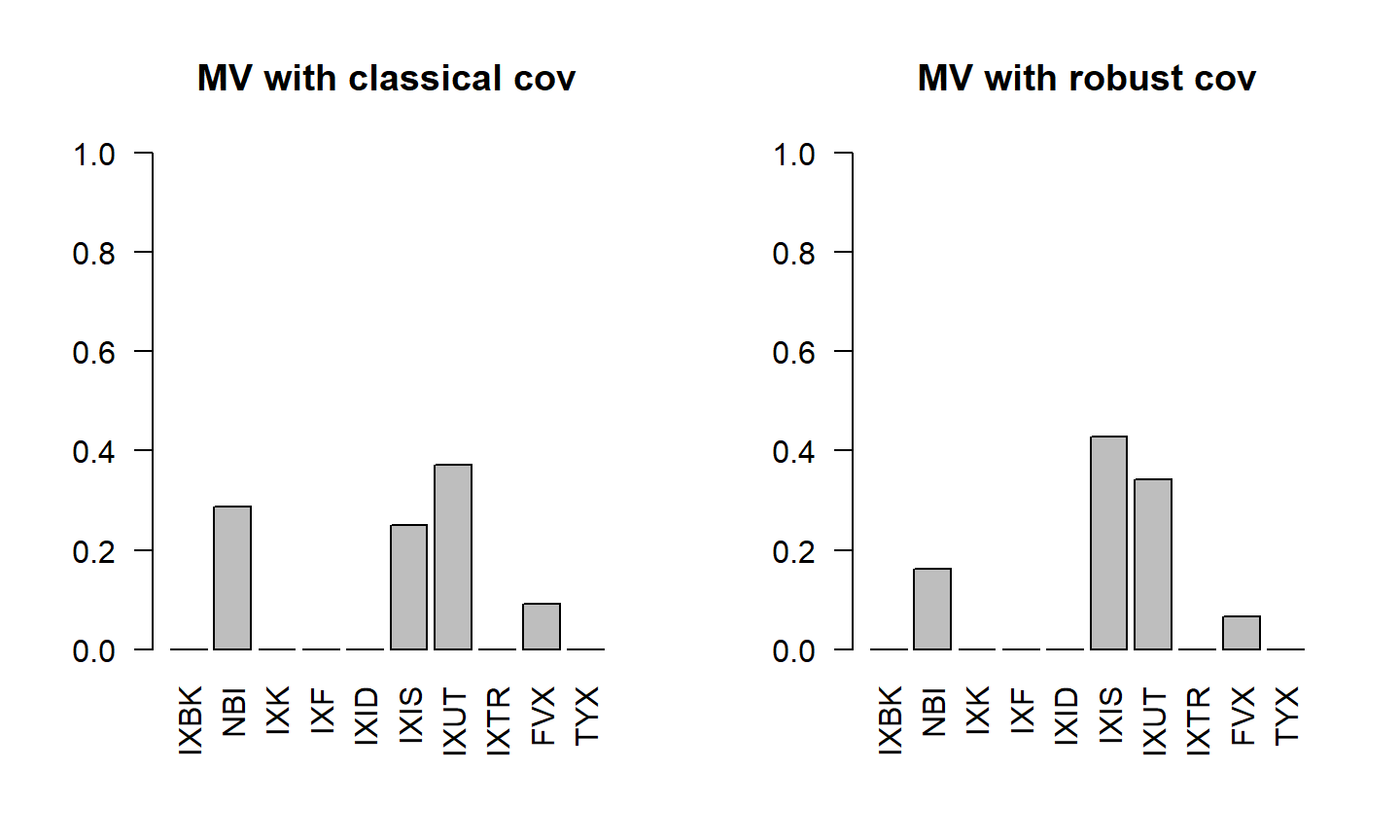
• Uma desvantagem do Modelo de Média-Variância é o uso da matriz de covariância para estimar o risco.

• O problema é que a matriz de covariância amostral é sensível à presença de outliers, que aparecem frequentemente em dados financeiros.

• Como passamos a matriz de covariância Sigma=cov(x) como argumento para a função MV_QP(), uma modificação simples do Modelo de Média-Variância é utilizar um estimador de covariância mais robusto.

• Vamos usar a função covMcd(), do pacote robustbase, que implementa o método do determinante de covariância mínima (Minimum Covariance Determinant) proposto por Rousseeuw & Driessen (1999). Esse método fornece um estimador mais robusto (menos sensível a outliers) para a covariância.

• Comparação dos pesos do método clássico e do método robusto:

• Outro ponto criticado do Modelo de Média-Variância é o uso do retorno médio dos componentes do portfólio como retorno alvo.

• Já foi mostrado que um erro no estimador da média pode suprimir os benefícios da otimização dos pesos, ou seja, um efeito de outliers no retorno médio pode levar a pesos inapropriados.

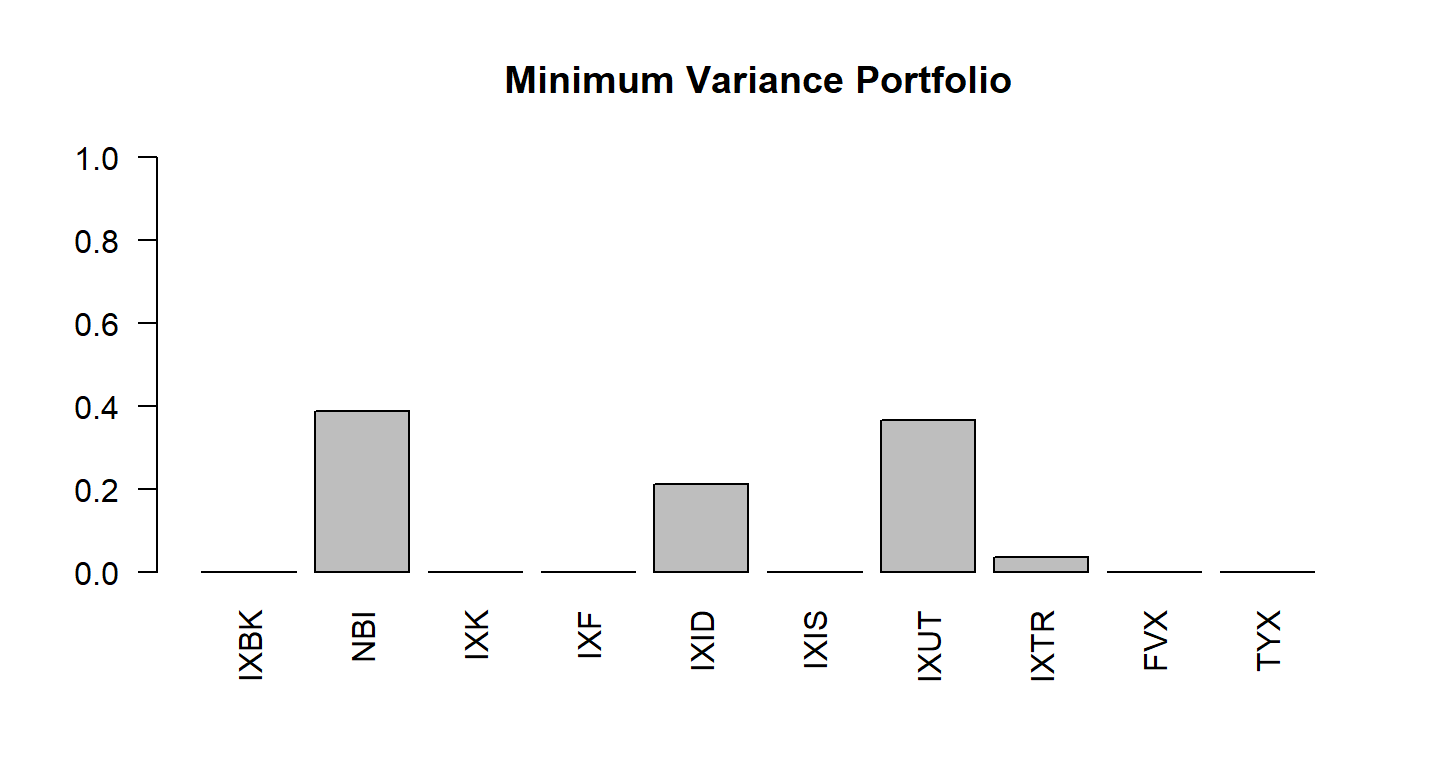
• Assim, podemos considerar um Modelo de Mínima Variância que otimiza os pesos apenas levando em conta a minimização da covariância sem fixar o retorno alvo.

## Modelo de Mínima Variância
w <- MV_QP(x, cstr = c(fullInvest(x), longOnly(x)))

• Além da matriz de covariância, existem outras alternativas para a medida de risco. Uma medida popular é o VaR (Value-at-Risk).

• O VaR é uma medida de risco probabilística. Por exemplo, um VaR ao nível de \(p\%\) é o valor tal que a probabilidade de uma perda maior do que ele seja menor ou igual a \(p\).

• Mais detalhes e exemplos: Seção 13.5.5

• Os modelos que consideramos aqui têm apenas restrições lineares. No entanto, em alguns cenários, a alocação de pesos de um portfólio pode requerer otimização sob restrições não-lineares.

• Por exemplo, um investidor pode estar interessado em minimizar a redução do valor do seu portfólio. A definição de redução do valor do portfólio, e um exemplo podem ser vistos na Seção 13.5.6.

• Por fim, podemos estar interessados em comparar a performance de portfólios com alocações diferentes. Essas comparações podem ser feitas através das medidas de retorno e medidas de risco.

• Alguns exemplos de como fazer essas comparações estão na Seção 13.6.