Modelo Coletivo para Tarifação de Seguros
Modelo para a Frequência
Modelo Poisson
Exemplos
02 de junho de 2023
Aula de Hoje
Tarifação de Seguros
Vimos na Parte III do curso como calcular Seguros e Anuidades de Vida, isto é, contratos cujos pagamentos dependem de eventos incertos relacionados à mortalidade e sobrevivência de vidas.
Para calcular os prêmios desses seguros, precisamos determinar a distribuição de probabilidade da variável aleatória valor presente da perda futura da seguradora. Essa variável aleatória depende do tempo de vida futuro de um indivíduo, que é descrito através de uma tábua de vida.
E para calcular um seguro de carro? E um seguro residencial? E um plano de saúde? (Ramo Não-Vida)
Tarifação de Seguros
Para seguros do Ramo Não-Vida, vamos usar dados históricos para construir modelos de tarifação.
Vamos discutir o uso de Modelos Lineares Generalizados em um exemplo para tarifação de seguros de automóveis.
O objetivo é encontrar um prêmio a ser cobrado de um segurado para uma apólice anual, baseado em características observáveis do segurado (como idade ou gênero) ou do objeto segurado (modelo e ano do carro, por exemplo).
Modelo Coletivo
Modelo Coletivo
Princípio do valor esperado:
- o prêmio associado a um risco anual \(S\) é
\[\pi(S) = (1+\alpha).\mathbb{E}(S) \] onde \(\alpha>0\) representa algum tipo de carregamento, e \(S\) é a perda aleatória anual.
Modelo Coletivo
Seja \((N_t)\) o processo de contagem do número de sinistros ocorridos entre \([0,t]\), e \((Y_i)\) o valor da i-ésima indenização.
Então a perda total no período \([0,t]\) é:
\[S_t = \sum_{i=1}^{N_t} Y_i \] com \(S_t=0\) se \(N_t=0\).
Prêmio Puro
Se \(\alpha=0\), o prêmio é chamado de prêmio puro.
Cobrar o prêmio puro pode ser justificado pela Lei dos Grandes Números, se assumirmos que as perdas são independentes e identicamente distribuídas.
No entanto, de acordo com a Teoria da Ruína, sabemos que a ruína será inevitável quando não há carregamento.
Prêmio Puro
O primeiro passo é calcular \(\mathbb{E}(S)\) para \(S=S_1\), o total anual.
Se \(N=N_1\) (número de indenizações no ano) e \(Y_1,\dots,Y_N\) são independentes e as perdas \(Y_i\) são i.i.d., então
\[\pi = \mathbb{E}(S) = \mathbb{E}(N) \cdot \mathbb{E}(Y) \]
- O
prêmio puro anual é o produto de dois termos:
- a frequência anual \(\mathbb{E}(N)\);
- o custo médio das indenizações \(\mathbb{E}(Y)\).
Prêmio Puro considerando Heterogeneidade
O prêmio puro do slide anterior considera apenas a média geral para todos os segurados, assumindo um risco homogêneo.
No entanto, sabemos que um modelo mais realista seria considerar riscos diferentes, ou heterogeneidade.
Prêmio Puro considerando Heterogeneidade
Vamos considerar o caso em que a heterogeneidade pode ser observada através de uma variável binária \(Z\) (por exemplo, risco baixo e risco alto com probabilidade 50% em cada).
Vamos assumir que \(N\) tem uma distribuição Binomial, com probabilidade 10% ou 20% de acordo com \(Z\). E vamos considerar que a perda é determinística, \(Y=100\).
A seguradora tem duas opções:
a ) cobrar o mesmo prêmio para todos os segurados, \(\pi = \mathbb{E}(S) = \mathbb{E}(N) \cdot \mathbb{E}(Y) = 15\)
b ) cobrar um prêmio considerando a heterogeneidade, \(\pi(z) = \mathbb{E}(S|Z=z) = 10 \mbox{ ou } 20\) dependendo de \(z\).
Prêmio Puro considerando Heterogeneidade
Isso pode ser perigoso se existirem duas seguradoras com modelos diferentes de tarifação. Os segurados de baixo risco irão preferir a seguradora que cobrar de acordo com b), enquanto segurados de alto risco irão preferir a seguradora que cobrar a).
Por isso, a seguradora que não levar em conta a heterogeneidade, e não cobrar prêmios de acordo com as características individuais, não irá sobreviver em um mercado competitivo.
Nesse exemplo, a seguradora deve cobrar:
\[\pi(z) = \mathbb{E}(S|Z=z) = \mathbb{E}(N|Z=z) \cdot \mathbb{E}(Y|Z=z) \]
Prêmio Puro considerando Heterogeneidade
O problema é que a heterogeneidade nem sempre é totalmente observável.
Na prática, a seguradora poderá observar algumas informações, resumidas em um vetor \(\boldsymbol{X}\), relacionadas às características do segurado, do objeto segurado, etc.
Algumas dessas covariáveis podem fornecer uma boa aproximação para a variável latente \(Z\). Nesse caso, a seguradora deve cobrar:
\[\pi(\boldsymbol{x}) = \mathbb{E}(S|\boldsymbol{X}=\boldsymbol{x}) = \mathbb{E}(N|\boldsymbol{X}=\boldsymbol{x}) \cdot \mathbb{E}(Y|\boldsymbol{X}=\boldsymbol{x}) \]
Prêmio Puro considerando Heterogeneidade
Nosso objetivo é propor modelos para estimar:
\(\mathbb{E}(N|\boldsymbol{X}=\boldsymbol{x})\): a frequência esperada de indenizações para segurados com características \(\boldsymbol{x}\); e
\(\mathbb{E}(Y|\boldsymbol{X}=\boldsymbol{x})\): a severidade, ou custo médio das indenizações para segurados com características \(\boldsymbol{x}\).
Modelo para a Frequência
Modelo para a Frequência
Vamos começar considerando modelos para a frequência de indenizações \(\mathbb{E}(N|\boldsymbol{X}=\boldsymbol{x})\).
Como estamos falando de contagens de eventos, a primeira opção é considerar a distribuição de Poisson.
Modelo Poisson
Assuma que o número de indenizações para um segurado siga um Processo de Poisson homogêneo com intensidade \(\lambda\).
Isso quer dizer que o número de eventos tem incrementos independentes, e que a quantidade de indenizações observadas durante o intervalo de tempo \([t,t+h]\) tem distribuição Poisson(\(\lambda \cdot h\)).
Modelo Poisson
Exposição
Para um segurado \(i\), muitas vezes não temos o número de indenizações anual, isto é, \(N_i\) para o período \([0,1]\).
Mas normalmente temos no banco de dados o número observado de indenizações \(Y_i\) durante o período \([0,E_i]\), onde \(E_i\) é a exposição do segurado no ano.
\[Y_i \sim \mbox{Poisson}(\lambda \cdot E_i) \]
Modelo Poisson
Considere o modelo Poisson para um grupo de segurados em que todos tem a mesma intensidade \(\lambda\).
Para estimar \(\lambda\), podemos usar máxima verossimilhança:
\[\mathcal{L}(\lambda,\boldsymbol{Y},\boldsymbol{E}) = \prod_{i=1}^n \frac{e^{-\lambda. E_i}(\lambda.E_i)^{Y_i}}{Y_i!} \]
\[\hat{\lambda} = \frac{\sum_{i=1}^n Y_i}{\sum_{i=1}^n E_i} \]
Modelo Poisson
- Como já falamos antes, faz sentido pensar que \(\lambda\) dependa de características (covariáveis) de cada segurado.
\[Y_i \sim \mbox{Poisson}(\lambda_i \cdot E_i) \]
- Utilizando uma função de ligação logarítmica (\(\lambda_i = e^{\boldsymbol{X}'_i\boldsymbol{\beta}}\)):
\[Y_i \sim \mbox{Poisson}\left(e^{ \boldsymbol{X}'_i\boldsymbol{\beta} + \log(E_i)} \right) \]
- É importante notar o papel da Exposição nesse modelo! O termo \(\log(E_i)\) é chamado de offset e é incluído como se fosse uma covariável, mas sem coeficiente.
Modelo Poisson
Assim, para modelar a frequência anual de indenizações, ajustamos uma regressão de Poisson ao número observado de indenizações \(Y\), incluindo as covariáveis \(\boldsymbol{X}\) e o log da exposição \(\log(E_i)\) como offset.
Vamos considerar \(\lambda_i = \exp(\boldsymbol{X}'_i \boldsymbol{\beta})\) (para garantir a positividade).
A log-verossimilhança é dada por:
\[\log \mathcal{L}(\boldsymbol{\beta}; \boldsymbol{Y}, \boldsymbol{E}) = \sum_{i=1}^n \left[ Y_i \log(\lambda_i E_i) - (\lambda_i E_i) - \log(Y_i!) \right] \\ \hspace{6cm} = \sum_{i=1}^n \left[ Y_i \cdot \left( \boldsymbol{X}'_i \boldsymbol{\beta} + E_i \right) - \exp\left\{ \boldsymbol{X}'_i \boldsymbol{\beta} + \log(E_i) \right\} - \log(Y_i!) \right] \]
Modelo Poisson
O estimador de máxima verossimilhança para \(\boldsymbol{\beta}\) pode ser encontrado numericamente usando o algoritmo de Newton-Raphson.
Esse método está implementado na função
glmdo R.
glm(Y~X1+X2+X3+offset(E), family=poisson(link="log"))
Exemplo
Vamos considerar o banco de dados
freMTPLfreqde seguros automobilísticos contra terceiros na França.Carregue os dados e veja as variáveis disponíveis.
Exemplo
- Antes de ajustar o modelo, vamos categorizar algumas variáveis:
## categorizando variáveis freMTPLfreq.f <- freMTPLfreq freMTPLfreq.f$DriverAge <- cut(freMTPLfreq$DriverAge,c(17,22,26,42,74,Inf)) freMTPLfreq.f$CarAge <- cut(freMTPLfreq$CarAge,c(0,1,4,15,Inf),include.lowest=TRUE) freMTPLfreq.f$Density <- cut(freMTPLfreq$Density,c(0,40,200,500,4500,Inf),include.lowest=TRUE) ## verificando as classes de cada variável summary(freMTPLfreq.f)
Exemplo
Ajuste um modelo de Poisson para o número de indenizações, considerando a exposição (log) como offset, e as covariáveis:
tipo de combustível;
idade do motorista;
e a densidade populacional da cidade.
(Obs: considere as variáveis categorizadas)
Exemplo
## ## Call: ## glm(formula = ClaimNb ~ Gas + DriverAge + Density + offset(log(Exposure)), ## family = poisson, data = freMTPLfreq.f) ## ## Deviance Residuals: ## Min 1Q Median 3Q Max ## -0.7655 -0.3385 -0.2669 -0.1488 6.5202 ## ## Coefficients: ## Estimate Std. Error z value Pr(>|z|) ## (Intercept) -1.86471 0.04047 -46.079 < 2e-16 *** ## GasRegular -0.20598 0.01603 -12.846 < 2e-16 *** ## DriverAge(22,26] -0.61606 0.04608 -13.370 < 2e-16 *** ## DriverAge(26,42] -1.07967 0.03640 -29.657 < 2e-16 *** ## DriverAge(42,74] -1.07765 0.03549 -30.362 < 2e-16 *** ## DriverAge(74,Inf] -1.10706 0.05188 -21.338 < 2e-16 *** ## Density(40,200] 0.18473 0.02675 6.905 5.02e-12 *** ## Density(200,500] 0.31822 0.02966 10.730 < 2e-16 *** ## Density(500,4.5e+03] 0.52694 0.02593 20.320 < 2e-16 *** ## Density(4.5e+03,Inf] 0.63717 0.03482 18.300 < 2e-16 *** ## --- ## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 ## ## (Dispersion parameter for poisson family taken to be 1) ## ## Null deviance: 105613 on 413168 degrees of freedom ## Residual deviance: 103986 on 413159 degrees of freedom ## AIC: 135263 ## ## Number of Fisher Scoring iterations: 6
Tarifação
Modelo com uma variável categórica
- Vamos considerar apenas uma covariável: tipo de combustível (diesel ou regular).
vY <- freMTPLfreq.f$ClaimNb # selecionando Y vE <- freMTPLfreq.f$Exposure # selecionando E X1 <- freMTPLfreq.f$Gas # selecionando X1
## Frequência de indenizações por tipo de combustível tapply(vY, X1, sum)/tapply(vE, X1, sum)
## Diesel Regular ## 0.07467412 0.06515364
Tarifação
Modelo com uma variável categórica
- Vamos ajustar um modelo de Poisson com essa covariável e sem intercepto:
## modelo sem intercepto df <- data.frame(vY,vE,X1) regpoislog <- glm(vY~0+X1+offset(log(vE)),data=df,family=poisson(link="log")) summary(regpoislog)
Tarifação
Modelo com uma variável categórica
- Interpretando os coeficientes:
## exponencial dos coeficientes ## exp(coef(regpoislog))
## X1Diesel X1Regular ## 0.07467412 0.06515364
Tarifação
Modelo com uma variável categórica
- Modelo com intercepto:
## modelo com intercepto regpoislog <- glm(vY~X1+offset(log(vE)),data=df,family=poisson(link="log")) summary(regpoislog)
- Interpretando os coeficientes:
## exponencial dos coeficientes ## exp(coef(regpoislog))
## (Intercept) X1Regular ## 0.07467412 0.87250624
Tarifação
Modelo com uma variável categórica
Nesse modelo, a categoria de referência é
Dieselque tem frequência de 0,0746.Para tipo de combustível
Regular, a frequência seria 87,25% da categoria de referência (igual a 0,0651).Essa seria a frequência estimada para calcular o prêmio.
Tarifação
Modelo com covariáveis contínuas
- Categorizamos algumas variáveis arbitrariamente. E se quisermos trabalhar com as variáveis contínuas?
Exercício:
Ajuste um modelo de Poisson incluindo apenas a idade categorizada do motorista como covariável (e o offset).
Compare esse ajuste com um modelo com a idade contínua.
Tarifação
Modelo com covariáveis contínuas
Uma limitação desse modelo é restringir a uma relação linear entre o número de indenizações e a idade.
Alternativas:
considerar idade como um fator (uma categoria diferente para cada idade):
as.factor(DriverAge)modelo não-paramétrico incluindo uma função \(s(X)\) da idade, onde \(s()\) pode ser um spline (curva definida entre dois nós). Esse modelo pode ser implementado com a função
gamdo pacotemgcv.
Tarifação
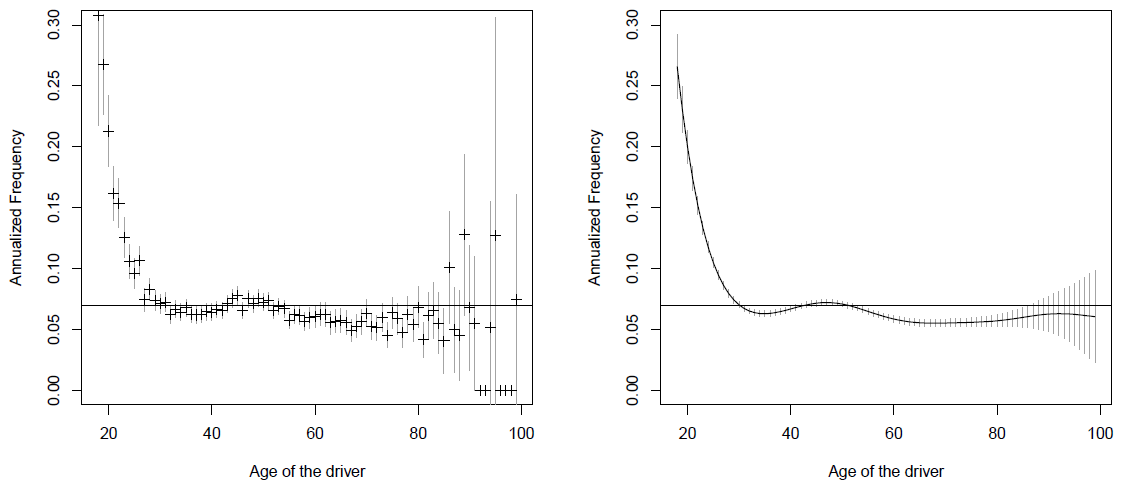
- Comparação entre a predição dos modelos para idade:
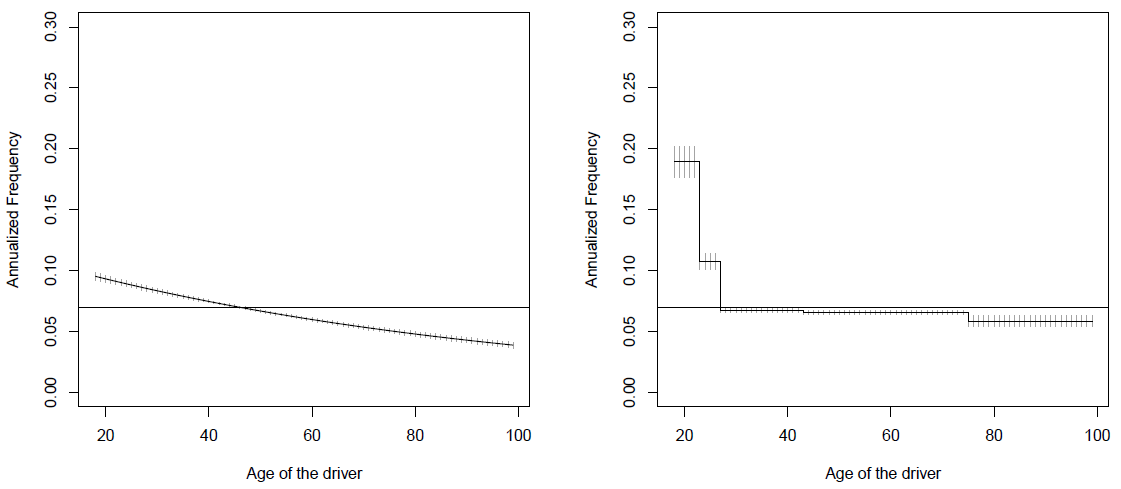
Tarifação