Alternativas para Modelo para a Frequência
Modelos para a Severidade
Modelos conjuntos para Frequência e Severidade
02 de junho de 2023
Aula de Hoje
Tarifação de Seguros
Vimos na aula passada como construir um modelo para encontrar o prêmio puro de acordo com um modelo coletivo para a perda financeira coberta por um seguro.
Vimos também que para uma seguradora ser competitiva, ela precisa levar em conta as informações disponíveis (covariáveis) para obter uma estimativa mais precisa para a perda média de cada contrato.
\[\pi(\boldsymbol x) = \mathbb{E}(N|\boldsymbol X = \boldsymbol x) \cdot \mathbb{E}(Y|\boldsymbol X = \boldsymbol x) \]
Tarifação de Seguros
Uma opção é modelar cada termo separadamente:
\(\mathbb{E}(N | \boldsymbol{X}=\boldsymbol{x})\): frequência esperada de indenizações para segurados com características \(\boldsymbol{x}\); e
\(\mathbb{E}(Y | \boldsymbol{X}=\boldsymbol{x})\): severidade, ou custo médio das indenizações para segurados com característica \(\boldsymbol{x}\).
Modelos para a Frequência
O modelo mais natural para a frequência (número esperado de indenizações) é o Poisson.
Limitação: ao assumir que \(Y_i \sim \mbox{Poisson}(\lambda_i.\,E_i)\), temos que \(\mathbb{E}(Y_i) = \mbox{Var}(Y_i) = \lambda_i.\,E_i\).
Uma alternativa é modelar a variância como:
\[\mbox{Var}(Y_i) = \phi .\, \mu_i \]
- Outras alternativas para a variância: Seções 14.3.1 – 14.3.4 do livro.
Modelos para a Frequência
Também podemos assumir outras distribuições de probabilidade para \(Y_i\), como:
Binomial Negativa (Seção 14.4.1);
Poisson/Binomial Negativa inflacionada em zero (Seção 14.4.2);
outras (Seção 14.4.3).
Veja as seções indicadas para funções e exemplos para estimar os parâmetros de acordo com esses modelos.
Modelos para a Severidade
Modelos para a Severidade
Vamos agora ver modelos apropriados para a severidade \(\mathbb{E}(Y|\boldsymbol{X}=\boldsymbol{x})\).
As ferramentas são as mesmas de antes: Modelos Lineares Generalizados.
Além disso, normalmente as covariáveis são mais informativas para prever a frequência do que a severidade.
Modelos para a Severidade
Exemplo
- Vamos continuar com o exemplo do banco de dados da aula passada.
Carregar o banco de dados
freMTPLfreqcom os dados de frequência, exposição e as covariáveis (motor do carro, idade do carro, idade do motorista, modelo do carro, tipo de combustível, região da residência, densidade populacional).Carregar o banco de dados
freMTPLsevcom os dados de severidade (valor das indenizações) para as apólices em que houve sinistro. Quais são as variáveis disponíveis nesse banco?
Modelos para a Severidade
Exemplo
## tamanho dos bancos dim(freMTPLfreq)
## [1] 413169 10
dim(freMTPLsev) # nem todas as apólices tiveram indenizações
## [1] 16181 2
sum(freMTPLfreq$ClaimNb>0)
## [1] 15390
Modelos para a Severidade
Exemplo
ids = freMTPLsev$PolicyID # apólices com indenizações length(ids)
## [1] 16181
length(unique(ids))
## [1] 15390
sum(freMTPLfreq$PolicyID %in% ids)
## [1] 15390
Modelos para a Severidade
Exemplo
## distribuição da severidade summary(freMTPLsev$ClaimAmount)
## Min. 1st Qu. Median Mean 3rd Qu. Max. ## 2 698 1156 2130 1243 2036833
Modelos para a Severidade
Exemplo
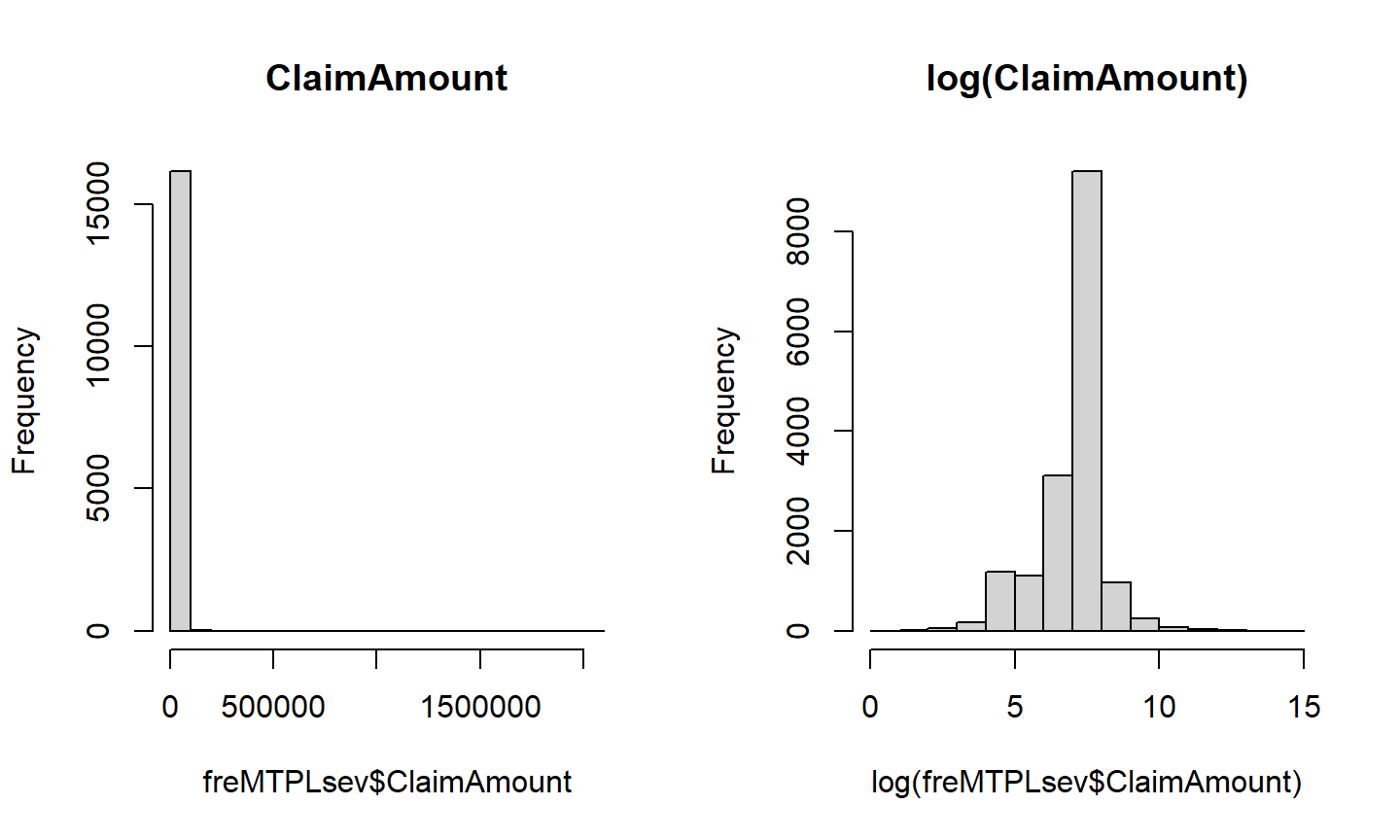
Modelos para a Severidade
- Vamos unificar os bancos para analisar a relação entre o valor das indenizações e as outras características das apólices.
## Unificando os bancos claims <- merge(freMTPLsev, freMTPLfreq) claims.f <- merge(freMTPLsev, freMTPLfreq.f)
- Qual a dimensão dos bancos resultantes? Quais variáveis estão incluídas nesses bancos? Como a função
mergeunifica os bancos?
Modelos para a Severidade
Como vimos anteriormente, selecionamos apenas as apólices em que houve pagamento de indenizações.
- Veja nos valores da variável
ClaimAmountdos bancos de dados que acabamos de criar.
- Veja nos valores da variável
- Agora, queremos um modelo que explique a variabilidade das indenizações de acordo com as covariáveis.
- Por isso, precisamos de distribuições estatísticas que assumam apenas valores positivos.
Regressão Gama
- \(Y\) tem distribuição Gama se a densidade pode ser escrita como:
\[f(y) = \frac{1}{y.\, \Gamma(\varphi^{-1})} \left( \frac{y}{\mu \varphi}\right)^{\varphi^{-1}} \exp \left( - \frac{y}{\mu \varphi}\right), \quad \forall \, y \in \mathbb{R}_{+}. \]
- A distribuição Gama pertence à família exponencial, e a função de ligação canônica é a inversa. Outras funções de ligação: identidade e logarítmo.
Regressão Log-Normal
- \(Y\) tem distribuição log-normal se a densidade pode ser escrita como:
\[f(y) = \frac{1}{y \sqrt{2 \pi \sigma^2}} \exp\left\{ - \frac{(\ln y - \mu)^2}{2 \sigma^2}\right\}, \quad \forall \, y \in \mathbb{R}_{+}. \]
- Podemos ajustar esse modelo considerando que \(Y\sim\mbox{Lognormal}\) se \(\log(Y)\sim\mbox{Normal}\).
Modelos para a Severidade
Exemplo
## Regressão Gama (para indenizações menores)
reg.gamma <- glm(ClaimAmount ~ CarAge + Gas, family=Gamma(link="log"),
data=claims[claims$ClaimAmount<15000,])
summary(reg.gamma)
## Regressão Log-Normal
reg.logn <- lm(log(ClaimAmount) ~ CarAge + Gas,
data=claims[claims$ClaimAmount<15000,])
summary(reg.logn)
Modelos para a Severidade
Outra alternativa: Normal Inversa
O ajuste dos modelos deve ser comparado usando os instrumentos padrões de Modelos Lineares Generalizados.
Modelando grandes valores
Se os valores das indenizações não forem muito grandes, as regressões gama e log-normal serão bem próximas (como vimos no exemplo anterior).
No entanto, quando temos indenizações com valores grandes, os ajustes serão diferentes.
Modelando grandes valores
Exemplo
## Regressão Gama (para todos os valores)
reg.gamma <- glm(ClaimAmount ~ DriverAge,
family=Gamma(link="log"), data=claims)
summary(reg.gamma)
## Regressão Log-Normal
reg.logn <- lm(log(ClaimAmount) ~ DriverAge, data=claims)
summary(reg.logn)
Modelando grandes valores
Exemplo
Nesse caso, os coeficientes são significativos nos dois modelos, mas com sinais diferentes (o efeito de aumentar a idade será diferente).
Isso acontece porque os outliers irão afetar o ajuste dos modelos.
Para isso, seria necessário considerar modelos mais robustos para a tarifação. Para mais discussão sobre isso: Seção 14.6.
Modelos conjuntos para Frequência e Severidade
Modelos conjuntos para Frequência e Severidade
Vamos finalizar considerando um modelo conjunto para frequência e severidade.
A alternativa mais comum é o modelo Tweedie.
A distribuição Tweedie pertence à família exponencial e satisfaz a seguinte condição:
\[\mbox{Var}(Y) = \varphi\,.[\mathbb{E}(Y)]^p \]
Modelo Tweedie
Se \(p=0\), temos uma distribuição com a variância constante (dist. normal);
Se \(p=1\), então a variância é linear (dist. Poisson);
Se \(p=2\), temos uma função de variância quadrática (dist. Gama);
Se \(p \in (1,2)\), então \(Y\) tem uma distribuição composta Poisson-Gama.
Modelo Tweedie
Exemplo
- Ajustando o modelo Tweedie com o pacote
tweedie:
Encontrar o valor de \(p\): usar a função
tweedie.profilepara encontrar o EMV para \(p\) para um determinado modelo.Usar o valor para estimar a regressão: função
glm(..., family=tweedie(var.power=p)).
- Outro pacote:
cplm.